Абстрактные (определяемые пользователями) типы данных
На самом деле, оба термина, употребленные в названии раздела, плохо отражают суть соответствующего понятия. Термин "абстрактные типы" плох тем, что реально ничего абстрактного в этой категории типов нет. Термин "определяемые пользователями типы" не точно отражает специфику, поскольку все типы, обсуждавшиеся выше, кроме встроенных в языки программирования, так или иначе определяются пользователями. Тем не менее, в силу привычки, мы будем использовать в этом разделе словосочетание "абстрактные типы данных" (АТД).
Не обращая больше внимания на ущербность терминологии, займемся содержанием понятия АТД. Как мы видели, наличие перечисляемых, уточняемых и конструируемых типов данных в сочетании со средствами выделения динамической памяти позволяет конструировать и использовать структуры данных, достаточные для создания произвольно сложных программ. Ограниченность этих средств состоит в том, что при определении типов и создании структур невозможно зафиксировать правила их использования. Например, если определен структурный тип с полями salary, commissions и total в предположении, что для любой переменной этого типа поле total всегда будет содержать общую сумму выплат, то ничто не мешает по ошибке нарушить это условие (с точки зрения компилятора никакой ошибки нет) и получить неверные результаты работы программы.
Основной идеей АТД является то, что при его определении специфицируется не только структура значений типа, но и набор допустимых операций над переменными и значениями этого типа. В наиболее сильном случае доступ к внутренней структуре типа доступен только через его операции. В число операций обязаны входить один или несколько конструкторов значений типа.
Имеется много разновидностей языков с АТД, языковые средства которых весьма различаются. Кроме того, к этому семейству языков примыкают языки объектно-ориентированного программирования. По поводу них одни авторы (к числу которых относится и автор этой книги) полагают, что для них термин "язык объектно-ориентированного программирования" является модной заменой старого термина "язык с АТД". Другие находят между этими языковыми семействами много тонких отличий, часть которых считают серьезными. Мы не будем глубоко анализировать эти дискуссии, а обсудим некоторые базовые концепции, общие для обоих семейств.
B+-деревья
Схема организации классических B-деревьев проста и элегантна, но не очень хороша для практического использования. Прежде всего это связано с тем, что в большинстве практических применений необходимо хранить во внешней памяти не только ключи, но и записи. Поскольку в B-дереве элементы располагаются и во внутренних, и в листовых страницах, а размер записи может быть достаточно большим, внутренние страницы не могут содержать слишком много элементов, по причине дерево может быть довольно глубоким. Поэтому для доступа к ключам и записям, находящимся на нижних уровнях дерева, может потребоваться много обменов с внешней памятью. Во-вторых, на практике часто встречается потребность хранения и поиска ключей и записей переменного размера. Поэтому тот критерий, что в каждой странице B-дерева содержится не меньше n и не больше 2*n ключей, становится неприменимым.
Широкое практическое применение получила модификация механизма B-деревьев, которую принято называть B+-деревьями. Эти деревья похожи на обычные B-деревья. Они тоже сильно ветвистые, и длина пути от корня к любой листовой странице одна и та же. Но структура внутренних и листовых страниц различна. Внутренние страницы устроены так же, как у B-дерева, но в них хранятся только ключи (без записей) и ссылки на страницы-потомки. В листовых страницах хранятся все ключи, содержащиеся в дереве, вместе с записями, причем этот список упорядочен по возрастанию значения ключа (рисунок 5.6).
Поиск ключа всегда доходит до листовой страницы. Аналогично операции включения и исключения тоже начинаются с листовой страницы. Для применения переливания, расщепления и слияния используются критерии, основанные на уровне заполненности соответствующей страницы. Для более экономного и сбалансированного использования внешней памяти при реализации B+-деревьев иногда используют технику слияния трех соседних страниц в две и расщепления двух соседних страниц в три. Хотя B+-деревья хранят избыточную информацию (один ключ может храниться в двух страницах), они, очевидно, обладают меньшей глубиной, чем классические B-деревья, а для поиска любого ключа требуется одно и то же число обменов с внешней памятью.

(a) Структура внутренней страницы B+-дерева

(b) Структура листовой страницы B+-дерева
Рис. 5.6. Структуры страниц B+-дерева
Дополнительной полезной оптимизацией B+-деревьев является связывание листовых страниц в одно- или двунаправленный список. Это позволяет просматривать списки записей для заданного диапазона значений ключей с лишь одним прохождением дерева от корня к листу.
Деревья цифрового поиска
Методы цифрового поиска достаточно громоздки и плохо иллюстрируются. Поэтому мы кратко остановимся на наиболее простом механизме - бинарном дереве цифрового поиска. Как и в деревьях, обсуждавшихся в предыдущих разделах, в каждой вершине такого дерева хранится полный ключ, но переход по левой или правой ветви происходит не путем сравнения ключа-аргумента со значением ключа, хранящегося в вершине, а на основе значения очередного бита аргумента.
Поиск начинается от корня дерева. Если содержащийся в корневой вершине ключ не совпадает с аргументом поиска, то анализируется самый левый бит аргумента. Если он равен 0, происходит переход по левой ветви, если 1 - по правой. Если не обнаруживается совпадение ключа с аргументом поиска, то анализируется следующий бит аргумента и т.д., пока либо не будут проверены все биты аргумента, или мы не наткнемся на вершину с отсутствующей левой или правой ссылкой.
На рисунке 4.16 показан пример дерева цифрового поиска для некоторых заглавных букв латинского алфавита. Считается, что буквы кодируются в соответствии с кодовым набором ASCII, а для их представления и поиска используются 5 младших бит кода. Например, код буквы A равен 41(16), а представляться A будет как последовательность бит 00001.

Рис. 4.16.
Деревья оптимального поиска
В приводившихся выше рассуждениях по поводу организации деревьев поиска предполагалось, что вероятность поиска любого возможного ключа одна и та же, т.е. распределена равномерно. Но встречаются ситуации, в которых можно получить информацию о вероятности обращений к отдельным ключам. Обычно в таких случаях дерево поиска строится один раз, имеет неизменяемую структуру, в него не включаются новые ключи, и из него не исключаются существующие ключи. Примером соответствующего приложения является сканер компилятора, одной из задач которого является определение принадлежности очередного идентификатора к набору ключевых слов языка программирования. На основе сбора статистики при многочисленной компиляции программ можно получить достаточно точную информацию о частотах поиска по отдельным ключам.
Пусть дерево поиска содержит n вершин, и обозначим через pi вероятность обращения к i-той вершине, содержащей ключ ki. Сумма всех pi, естественно, равна 1. Постараемся теперь организовать дерево поиска таким образом, чтобы обеспечить минимальность общего числа шагов поиска, подсчитанного для достаточно большого количества обращений. Будем считать, что корень дерева имеет высоту 1 (а не 0, как раньше), и определим взвешенную длину пути дерева как сумму pi*hi (1<=i<=n), где hi - длина пути от корня до i-той вершины. Требуется построить дерево поиска с минимальной взвешенной длиной пути.
В качестве примера рассмотрим возможности построения дерева поиска для трех ключей 1, 2, 3 с вероятностями обращения к ним 1/7, 2/7 и 4/7 соответственно (рисунок 4.15).
Посчитаем взвешенную длину пути для каждого случая. В случае (a) взвешенная длина пути P(a) = 1*4/7 + 2*2/7 + 3*1/7 = 11/7. Аналогичные подсчеты дают результаты P(b)=12/7; P(c)=12/7; P(d)=15/7; P(e)=17/7. Следовательно, оптимальным в интересующем нас смысле оказалось не идеально сбалансированное дерево (c), а вырожденное дерево (a).
На практике приходится решать несколько более общую задачу, а именно, при построении дерева учитывать вероятности неудачного поиска, т.е.
поиска ключа, не включенного в дерево. В частности, при реализации сканера желательно уметь эффективно распознавать идентификаторы, которые не являются ключевыми словами. Можно считать, что поиск по ключу, отсутствующему в дереве, приводит к обращению к "специальной" вершине, включенной между реальными вершинами с меньшим и большим значениями ключа соответственно. Если известна вероятность qj обращения к специальной j-той вершине, то к общей средней взвешенной длине пути дерева необходимо добавить сумму qj*ej для всех специальных вершин, где ej - высота j-той специальной вершины.

(a)

(b)

(c)

(d)

(e)
Рис. 4.15. При построении дерева оптимального поиска вместо значений pi и qj обычно используют полученные статистически значения числа обращений к соответствующим вершинам. Процедура построения дерева оптимального поиска достаточно сложна и опирается на тот факт, что любое поддерево дерева оптимального поиска также обладает свойством оптимальности. Поэтому известный алгоритм строит дерево "снизу-вверх", т.е. от листьев к корню. Сложность этого алгоритма и расходы по памяти составляют O(n2). Имеется эвристический алгоритм, дающий дерево, близкое к оптимальному, со сложностью O(n*log n) и расходами памяти - O(n).
Динамическое распределение памяти и списки
При решении ряда задач становится неудобно, неэффективно, а иногда и просто невозможно обойтись использованием памяти, выделяемой компилятором и системой поддержки времени выполнения в соответствии с явными описаниями переменных в программе. Во всех языках, более или менее приспособленных к практическому применению, имеется возможность явно запрашивать и использовать области так называемой динамической памяти. Такие области принято называть "динамическими переменными". Возможности создания и использования динамических переменных тесно связаны с механизмами указателей, поскольку динамическая переменная не имеет статически заданного имени, и доступ к такой переменной возможен только через указатель.
Как и во многих обсуждавшихся ранее случаях, механизмы работы с динамической памятью в языках с сильной типизацией существенно отличаются от соответствующих механизмов языков со слабой типизацией. В языках линии Паскаль для запроса динамических переменных используется встроенная процедура new(var), где var - переменная некоторого ссылочного типа T. Если тип T определялся конструкцией type T = T0, то при выполнении этой процедуры подсистема поддержки времени выполнения выделяет динамическую область памяти с размером, достаточным для размещения переменных типа T0, и переменной var присваивается ссылочное значение, обеспечивающее доступ к выделенной динамической переменной.
Понятно, что размеры области памяти, используемой для динамического выделения переменных, в любой реализации языка ограничены. Кроме того, обычно время полезного существования динамической переменной меньше времени выполнения программы, в которой эта переменная была создана. Поэтому наряду со средствами образования динамических переменных должны существовать средства освобождения памяти, занятой ставшими бесполезными динамическими переменными. В сильно типизированных языках для этого применяются два разных механизма.
Первый - это явное использование встроенной процедуры dispose(var), где var - переменная ссылочного типа, значение которой указывает на ранее выделенную и еще не освобожденную динамическую переменную.
Тем самым, чтобы использовать значение, возвращаемое функцией malloc(), необходимо явно преобразовать его тип к нужному указательному типу. Для освобождения ранее выделенной области динамической памяти используется функция free(). Ее входным параметром является значение типа *void, которое должно указывать на начало ранее выделенной динамической области. Поведение программы непредсказуемо при использовании указателей на ранее освобожденную память и при задании в качестве параметра функции free() некорректного значения. Заметим, что по причине наличия возможности получить значение указателя на любую статически объявленную переменную, работа с указателями на статические и динамические переменные производится полностью единообразно. Единообразная работа с массивами и указателями естественным образом позволяет создавать и использовать динамические массивы. Как видно, с динамической памятью в языках Си/Си++ работать можно очень эффективно, но программирование является опасным. Используя структурные типы, указатели и динамические переменные, можно создавать разнообразные динамические структуры памяти - списки, деревья, графы и т.д. (Особенности указателей в языках Си/Си++ позволяют, вообще говоря, строить динамические структуры памяти на основе статически объявленных переменных или на смеси статических и динамических переменных.) Идея организации всех динамических структур одна и та же. Определяется некоторый структурный тип T, одно или несколько полей которого объявлены указателями на тот же или некоторый другой структурный тип. В программе объявляется переменная var типа T (или переменная типа указателя на T в случае полностью динамического создания структуры). Имя этой переменной при выполнении программы используется как имя "корня" динамической структуры. При выполнении программы по мере построения динамической структуры запрашиваются динамические переменные соответствующих типов и связываются ссылками, начиная с переменной var (или первой динамической переменной, указатель на которую содержится в переменной var).
Понятно, что этот подход позволяет создать динамическую структуру с любой топологией. Наиболее простой динамической структурой является однонаправленный список (рисунок 1.1). Для создания списка определяется структурный тип T, у которого имеется одно поле next, объявленное как указатель на T. Другие поля структуры содержат информацию, характеризующую элемент списка. При образовании первого элемента ("корня") списка в поле next заносится пустой указатель (nil или NULL). При дальнейшем построении списка это значение будет присутствовать в последнем элементе списка

Рис. 1.1. Над списком, построенном в такой манере, можно выполнять операции поиска элемента, удаления элемента и занесение нового элемента в начало, конец или середину списка. Понятно, что все эти операции будут выполняться путем манипуляций над содержимым поля next существующих элементов списка. Для оптимизации операций над списком иногда создают вспомогательную переменную-структуру (заголовок списка), состоящую из двух полей - указателей на первый и последний элементы списка (рисунок 1.2). Для этих же целей создают двунаправленные списки, элементы которых, помимо поля next, включают поле previous, содержащее указатель на предыдущий элемент списка (рисунок 1.3) и, возможно, ссылки на заголовок списка (рисунок 1.4).
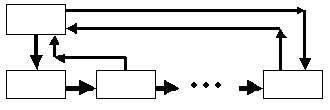
Рис. 1.2.
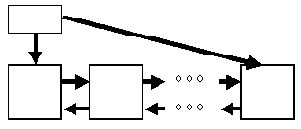
Рис. 1.3.
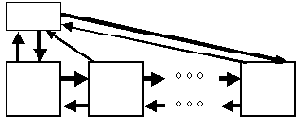
Рис. 1.4.
Дополнительные способы поддержки поиска в базах данных
Мы не будем глубоко вдаваться в методы, которые в настоящее время все более распространяются в области баз данных (поскольку в них нет ничего принципиально нового). Тем не менее, кажется оправданным сказать несколько слов по этому поводу.
Двоичные деревья
Для организации поиска в основной памяти особое значение имеют упорядоченные двоичные (бинарные) деревья (как, например, на рисунке 4.3). В каждом таком дереве естественно определяются левое и правое поддеревья. Двоичное дерево называется идеально сбалансированным, если число вершин в его левом и правом поддеревьях отличается не более, чем на 1 (легко видеть, что при соблюдении этого условия длины пути до любой листовой вершины дерева отличаются не больше, чем на 1). Примеры идеально сбалансированных деревьев показаны на рисунке 4.5.

Рис. 4.5.

Рис. 4.6.
Двоичные деревья обычно представляются как динамические структуры (см. раздел 1.7) с базовым типом записи T, в число полей которого входят два указателя на переменные типа T.
При использовании в целях поиска элементов данных по значению уникального ключа применяются двоичные деревья поиска, обладающие тем свойством, что для любой вершины дерева значение ее ключа больше значения ключа любой вершины ее левого поддерева и больше значения ключа любой вершины правого поддерева (рисунок 4.6). Для поиска заданного ключа в дереве поиска достаточно пройти по одному пути от корня до (возможно, листовой) вершины (рисунок 4.7). Высота идеально сбалансированного двоичного дерева с n вершинами составляет не более, чем log n (логарифм двоичный), поэтому при применении таких деревьев в качестве деревьев поиска (рисунок 4.8) потребуется не более log n сравнений.

Рис. 4.7. Путь поиска ключа по значению “23”

Рис. 4.8. Идеально сбалансированное двоичное дерево
Применение деревьев как объектов с динамической структурой особенно полезно, если допускать выполнение не только операции поиска по значению ключа, но и операций включения новых и исключения существующих ключей. Если не принимать во внимание потенциальное желание поддерживать идеальную балансировку дерева, то процедуры включения и исключения ключей очень просты. Для включения в дерево вершины с новым ключом x по общим правилам поиска ищется листовая вершина, в которой находился бы этот ключ, если бы он входил в дерево.
Возможны две ситуации: (a) такая вершина не существует; (b) вершина существует и уже занята, т.е. содержит некоторый ключ y. В первой ситуации создается недостающая вершина, и в нее заносится значение ключа x. Во второй ситуации после включения ключа x эта вершина в любом случае становится внутренней, причем если x > y, то ключ x заносится в новую листовую вершину - правого сына y, а если x < y - то в левую. Четыре потенциально возможных случая проиллюстрированы на рисунке 4.9.

(a)

(b)

(c)

(d)

(e)
Рис. 4.9. При выполнении исключения ключа из дерева также прежде всего выполняется поиск ключа. Если ключ обнаруживается, то возможны следующие случаи: (a) ключ содержится в листовой вершине, у вершины-отца которой имеются два сына; (b) ключ содержится в листовой вершине, являющей единственным сыном своего отца; (c) ключ содержится во внутренней вершине, имеющей только левого или только правого сына; (d) ключ содержится во внутренней вершине, имеющей и левого, и правого сыновей. В случае (a) соответствующая листовая вершина ликвидируется, а у ее отца остается только один сын. В случае (b) листовая вершина ликвидируется, а ее отец становится новой листовой вершиной. В случае (c) внутренняя вершина ликвидируется, и ее место занимает единственный сын (он может быть внутренней или листовой вершиной. В случае (d) внутренняя вершина ликвидируется, и заменяется на листовую или внутреннюю вершину, достигаемую по самому правому пути от левого сына внутренней вершины. Эта вершина наследует левого и правого сыновей ликвидируемой вершины. Возможные варианты иллюстрируются на рисунке 4.10.

(a)

(b)

(c)

(d)

(e)

(f)
Рис. 4.10. Исключение ключа из двоичного дерева Поддержка дерева поиска в идеально сбалансированном состоянии требует существенного усложнения (с соответствующим увеличением накладных расходов) операций включения и исключения ключей. Кроме того, как показано в книге Вирта, при равномерном распределении значений включаемых и исключаемых ключей использование идеально сбалансированных деревьев поиска дает выигрыш не более 30% (имеется в виду число сравнений, требующихся при поиске).Поэтому на практике идеально сбалансированные деревья поиска используются крайне редко.
Двойное хэширование
Для обеспечения равномерного распределения ключей в хэш-таблице при наличии коллизий можно применять метод двойного хэширования. Он состоит в том, что если при включении или поиска ключа в хэш-таблице возникает коллизия, то к ключу (или к комбинации ключа и текущего индекса массива) применяется вторичная хэш-функция, значение которой указывает циклическое смещение в массиве от текущего индекса к элементу, в который следует включать или в котором следует искать требуемую запись (рисунки 4.21, 4.22).

Рис. 4.21.
Поскольку метод двойного хэширования в полной форме приводит к слишком большим накладным расходам, на практике часто используется упрощенная форма этого метода, не гарантирующая равномерности записей в массиве, но обеспечивающая лучшие результаты, чем линейное зондирование. Один из способов состоит в использовании квадратичной функции при вычислении индекса следующей пробы. В этом случае последовательность вычисления индексов проб при включении или поиске записи является следующей: h0 = H(K) ........ hi = (h0 + i^2) MOD N (i>0)
Основным недостатком метода квадратичных проб является то, что для включаемой записи может не найтись свободного элемента массива даже в том случае, когда реально около половины элементов являются свободными.

Рис. 4.22.
Естественное слияние
При использовании метода прямого слияния не принимается во внимание то, что исходный файл может быть частично отсортированным, т.е. содержать упорядоченные подпоследовательности записей. Серией называется подпоследовательность записей ai, a(i+1), ..., aj такая, что ak <= a(k+1) для всех i <= k < j, ai < a(i-1) и aj > a(j+1). Метод естественного слияния основывается на распознавании серий при распределении и их использовании при последующем слиянии.
Как и в случае прямого слияния, сортировка выполняется за несколько шагов, в каждом из которых сначала выполняется распределение файла A по файлам B и C, а потом слияние B и C в файл A. При распределении распознается первая серия записей и переписывается в файл B, вторая - в файл C и т.д. При слиянии первая серия записей файла B сливается с первой серией файла C, вторая серия B со второй серией C и т.д. Если просмотр одного файла заканчивается раньше, чем просмотр другого (по причине разного числа серий), то остаток недопросмотренного файла целиком копируется в конец файла A. Процесс завершается, когда в файле A остается только одна серия. Пример сортировки файла показан на рисунках 3.1 и 3.2.
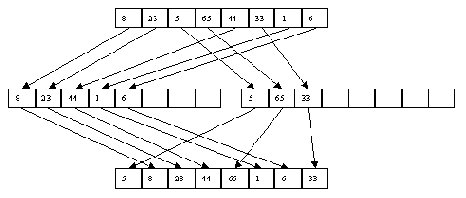
Рис. 3.1. Первый шаг
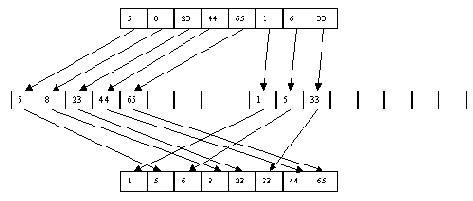
Рис. 3.2. Второй шаг
Очевидно, что число чтений/перезаписей файлов при использовании этого метода будет не хуже, чем при применении метода прямого слияния, а в среднем - лучше. С другой стороны, увеличивается число сравнений за счет тех, которые требуются для распознавания концов серий. Кроме того, поскольку длина серий может быть произвольной, то максимальный размер файлов B и C может быть близок к размеру файла A.
Индексы на основе использования битовых шкал
Начнем с определения списка RID. Каждой строке в таблице приписывается RID, который можно рассматривать как указатель на строку на диске. Обычно RID состоит из номера страницы на диске и номера позиции записи на этой странице. Набор строк с данным свойством может быть представлен как список RID этих строк. В большинстве СУБД используются 4-байтовые RID (хотя в Oracle RID имеет длину по крайней мере 6 байт). Традиционно списки RID использовались в индексах для определения набора строк, ассоциированных с каждым значением некоторого индексируемого столбца. Если предположить потребность в индексе на таблице SALES, содержащей 100 миллионов строк и включающей столбец department c 40 разными значениями, то для каждого значения этого столбца мы получим список RID, который в среднем будет соответствовать 2.5 миллионам строк.
При наличии громадного числа RID, ассоциированных с каждым значением department, трудно рассчитывать, что удастся целиком переместить список RID в основную память. Список разбивается на фрагменты по несколько сотен RID, которые могут быть помещены в последовательные листовые узлы B-дерева. Для каждого фрагмента можно хранить в B-дереве только одно значение department, так что критически остается лишь потребность в хранении 100 миллионов 4-байтовых RID.
Теперь мы готовы ввести идею битовой индексации. В таблице, для которой используется эта техника, все строки должны быть перенумерованы: 0, 1, 2, ..., N-1. Нумерация строк должна производиться в соответствии с порядком их RID (физически последовательно относительно расположения строк на диске). Требуется метод преобразования номера строки в RID и наоборот. Теперь, если имеется последовательность из N бит, установим k-тый бит в 1, если строка с номером k входит в набор строк, а в противном случае - в 0. Битовый индекс на SALES по столбцу department аналогичен тому, который основан на RID, но вместо фрагментов RID в нем используются соответствующие битовые фрагменты. Каждый битовый фрагмент будет занимать 12.5 Мб, так что вполне вероятно разместить его на последовательных страницах диска.
Отношение числа битов, установленных в 1, к общей длине набора бит называется плотностью этого набора и аналогично селективности условия выборки. Фрагменты с низкой плотностью можно компрессировать. Пока же будем считать, что все фрагменты обладают высокой плотностью. В этом случае полный битовый индекс требует на листовом уровне чуть больше 500 Мб внешней памяти, т.е. больше, чем индекс, основанный на RID. Однако, ситуация меняется, если индексируемый столбец содержит мало различных значений. Если, например, таблица SALES содержит столбец gender (пол) со всего двумя значениями M и F, то для листового уровня битового индекса потребуется всего 25 Мб, в то время как для RID-индекса по-прежнему было бы нужно иметь 400 Мб. Для индексов с менее, чем 32 значениями битовые индексы позволяют экономить память. Однако, наиболее важным свойством неупакованных битовых индексов является не экономия памяти, а возможность существенно повысить скорость выполнения операций AND, OR, NOT и COUNT. Предположим, что имеются два битовых фрагмента B1 и B2, где B1 представляет свойство gender = 'M', а B2 - department = 'sports'. Тогда для получения битового фрагмента, соответствующего свойству B1 & B2, требуется всего лишь выполнить поразрядное логическое умножение B1 и B2. Для выполнения операции AND над двумя списками RID требуется более сложная техника: слияние с пересечением. Нужно использовать два курсора, каждый из которых продвигается по одному из списков, и в результирующем списке остаются те RID, которые встречаются в каждом из исходных списков. Конечно, если списки-операнды включают только по несколько десятков RID, то цикл со списками RID окажется более эффективным, чем цикл, в котором выполняется логическое умножение битовых шкал, длина каждой из которых равна общему числу строк в таблице. Но при плотности битовой шкалы большей, чем 1/100, алгоритм на основе битовых шкал работает быстрее. Аналогично обстоят дела с алгоритмами для выполнения операций OR, NOT и COUNT. Если битовая шкала становится очень разреженной, то битовые индексы работают плохо по сравнению с RID-индексами не только в связи с нагрузкой на процессор, но и по причине большого числа обменов с внешней памятью.Для решения обеих проблем требуется какой-либо метод сжатия, который позволил бы сократить расходы внешней памяти, но в то же время позволил бы по-прежнему быстро выполнять операции AND, OR, NOT и COUNT. Один из подходов состоит в совместном использовании битовой и RID индексации: когда битовый фрагмент становится слишком разреженным, он заменяется на RID-фрагмент. В других подходах используется техника кодирования битовых шкал. В этом случае становится сложно эффективно выполнять перечисленные выше операции между сжатой и несжатой шкалами. Потребность нахождения техники сжатия, которая бы не тормозила выполнение этих операций, является наиболее важной проблемой битовой индексации.
Индексы соединения
Это очень простая идея. Она происходит от классической экспериментальной системы IBM System R. Если можно создавать индексы для отдельных таблиц, то почему нельзя делать индексы для нескольких таблиц? Индексировать совместно таблицы, которые требуется соединять? Обычно используют обычные B+-деревья. В поле записи этих деревьев содержится список идентификаторов записей соединяемых таблиц.
Достаточно дорогой, но очень эффективный метод поддержки соединений.
Инкапсуляция
Существуют разные точки зрения относительно того, для чего наиболее полезно применять абстрактные типы данных. Многие считают, например, что основной смысл этого подхода состоит в развитии методов модульного структурного программирования. Это, конечно, верно, но с точки зрения автора наибольшее преимущество подхода абстрактных типов данных состоит в принципиальном разделении спецификации и реализации типа. Для правильного написания (а иногда и отладки) программы достаточно иметь набор спецификаций требуемых типов. Для каждой спецификации, вообще говоря, может существовать несколько реализаций, и при их корректном создании эти реализации могут быть взаимозаменяемыми.
В строго типизированных языках с абстрактными типами данных спецификация типа скрывает его реализацию. Внешнее представление типа инкапсулирует особенности его структурной и операционной реализации. До сих пор продолжаются споры о том, что является идеальной инкапсуляцией типа. В частности, многие полагают, что разрешение прямого доступа к переменным состояния нарушает принципы инкапсуляции. По всей видимости, это неверно. Если все возможные операции со значениями типа строго специфицированы в его внешнем представлении, то в любом случае могут допускаться различные реализации типа. Но, естественно, чем более высоким уровнем обладает спецификация, тем больше свобода при выборе реализации.
Использование цепочек переполнения
Это один из наиболее очевидных способов разрешения коллизий. Если по смыслу в элементах массива хранятся записи типа T, то в данном случае к записи добавляется поле типа ссылки на T. При возникновении коллизии по причине включения новой записи для нового элемента выделяется динамическая память, и он включается в конец линейного списка, который начинается от первичного элемента массива. Если коллизия возникает при поиске ключа, то список переполнения просматривается либо до момента нахождения требуемого ключа, либо до конца, что означает отсутствие искомой записи (рисунок 4.23).

Рис. 4.23.
Метод цепочек переполнения легко реализуется, понятен, но потенциально приводит к излишним расходам памяти.
Использование хэширования для организации индексов в базах данных
Методы хэширования в базах данных используются пока не очень часто. Одним из уникальных примеров систем, где с самого начала применяются методы хэширования, является Ingres. Причины понятны. Хэширование с самого возникновения ориентировано на поиск по уникальному ключу. Наиболее распространенные методы не могут обеспечить, например, поиск записей для заданного диапазона значений ключа. Тем не менее, похоже, что технология хэширования постепенно сольется с технологией B-деревьев и станет основной в мире баз данных.
Классические B-деревья
Механизм классических B-деревьев был предложен в 1970 г. Бэйером и Маккрейтом. B-дерево порядка n представляет собой совокупность иерархически связанных страниц внешней памяти (каждая вершина дерева - страница), обладающая следующими свойствами: Каждая страница содержит не более 2*n элементов (записей с ключом). Каждая страница, кроме корневой, содержит не менее n элементов. Если внутренняя (не листовая) вершина B-дерева содержит m ключей, то у нее имеется m+1 страниц-потомков. Все листовые страницы находятся на одном уровне.
Пример B-дерева степени 2 глубины 3 приведен на рисунке 5.1.

Рис. 5.1. Классическое B-дерево порядка 2
Поиск в B-дереве производится очевидным образом. Предположим, что происходит поиск ключа K. В основную память считывается корневая страница B-дерева. Предположим, что она содержит ключи k1, k2, ..., km и ссылки на страницы p0, p1, ..., pm. В ней последовательно (или с помощью какого-либо другого метода поиска в основной памяти) ищется ключ K. Если он обнаруживается, поиск завершен. Иначе возможны три ситуации: Если в считанной странице обнаруживается пара ключей ki и k(i+1) такая, что ki < K < k(i+1), то поиск продолжается на странице pi. Если обнаруживается, что K > km, то поиск продолжается на странице pm. Если обнаруживается, что K < k1, то поиск продолжается на странице p0.
Для внутренних страниц поиск продолжается аналогичным образом, пока либо не будет найден ключ K, либо мы не дойдем до листовой страницы. Если ключ не находится и в листовой странице, значит ключ K в B-дереве отсутствует.
Включение нового ключа K в B-дерево выполняется следующим образом. По описанным раньше правилам производится поиск ключа K. Поскольку этот ключ в дереве отсутствует, найти его не удастся, и поиск закончится в некоторой листовой странице A. Далее возможны два случая. Если A содержит менее 2*n ключей, то ключ K просто помещается на свое место, определяемое порядком сортировки ключей в странице A. Если же страница A уже заполнена, то работает процедура расщепления.
Заводится новая страница C. Ключи из страницы A (берутся 2*n-1 ключей) + ключ K поровну распределяются между A и C, а средний ключ вместе со ссылкой на страницу C переносится в непосредственно родительскую страницу B. Конечно, страница B может оказаться переполненной, рекурсивно сработает процедура расщепления и т.д., вообще говоря, до корня дерева. Если расщепляется корень, то образуется новая корневая вершина, и высота дерева увеличивается на единицу. Одношаговое включение ключа с расщеплением страницы показано на рисунке 5.2.

(a) Попытка вставить ключ 23 в уже заполненную страницу

(b) Выполнение включения ключа 22 путем расщепления страницы A
Рис. 5.2. Пример включения ключа в B-дерево Процедура исключения ключа из классического B-дерева более сложна. Приходится различать два случая - удаление ключа из листовой страницы и удаления ключа из внутренней страницы B-дерева. В первом случае удаление производится просто: ключ просто исключается из списка ключей. При удалении ключа во втором случае для сохранения корректной структуры B-дерева его необходимо заменить на минимальный ключ листовой страницы, к которой ведет последовательность ссылок, начиная от правой ссылки от ключа K (это минимальный содержащийся в дереве ключ, значение которого больше значения K). Тем самым, этот ключ будет изъят из листовой страницы (рисунок 5.3).

(a) Начальный вид B-дерева

(b) B-дерево после удаления ключа 25
Рис. 5.3. Пример исключения ключа из B-дерева Поскольку в любом случае в одной из листовых страниц число ключей уменьшается на единицу, может нарушиться то требование, что любая, кроме корневой, страница B-дерева должна содержать не меньше n ключей. Если это действительно случается, начинает работать процедура переливания ключей. Берется одна из соседних листовых страниц (с общей страницей-предком); ключи, содержащиеся в этих страницах, а также средний ключ страницы-предка поровну распределяются между листовыми страницами, и новый средний ключ заменяет тот, который был заимствован у страницы-предка (рисунок 5.4).

Рис. 5.4. Результат удаления ключа 38 из B-дерева с рисунка 5.3 Может оказаться, что ни одна из соседних страниц непригодна для переливания, поскольку содержат по n ключей. Тогда выполняется процедура слияния соседних листовых страниц. К 2*n-1 ключам соседних листовых страниц добавляется средний ключ из страницы-предка (из страницы-предка он изымается), и все эти ключи формируют новое содержимое исходной листовой страницы. Поскольку в странице-предке число ключей уменьшилось на единицу, может оказаться, что число элементов в ней стало меньше n, и тогда на этом уровне выполняется процедура переливания, а возможно, и слияния. Так может продолжаться до внутренних страниц, находящихся непосредственно под корнем B-дерева. Если таких страниц всего две, и они сливаются, то единственная общая страница образует новый корень. Высота дерева уменьшается на единицу, но по-прежнему длина пути до любого листа одна и та же. Пример удаления ключа со слиянием листовых страниц показан на рисунке 5.5.

(a) Начальный вид B-дерева

(b) B-дерево после удаления ключа 29
Рис. 5.5. Пример удаления ключа из B-дерева со слиянием листовых страниц
Коллизии при хэшировании и способы их разрешения
Хэширование может обеспечить хорошие результаты и в том случае, когда набор ключей заранее неизвестен. В этом случае не приходится говорить о генерации совершенной хэш-функции. Даже если известен диапазон значений ключей, то в лучшем случае применение совершенного хэширования потребует наличия в памяти массива с размером, равным мощности множества ключей. Кроме того, неизвестны выполняемые в разумное время алгоритмы генерации совершенной хэш-функции для множества ключей большой мощности.
Распространенным методом является использование эмпирически подобранной хэш-функции, которая (a) по значению ключа производит значение индекса в границах массива и (b) равномерно распределяет ключи по элементам массива. Если ORD(k) обозначает порядковый номер ключа k в упорядоченном множестве допустимых ключей, а N - число элементов в массиве записей, то одной из наиболее естественных хэш-функций является H(k) = ORD(k) MOD N, т.е. взятие остатка от деления порядкового номера ключа на число элементов массива. Такая функция выполняется очень быстро, если N является степенью числа 2. Для числовых ключей функция обеспечивает достаточную равномерность распределения ключей в массиве.
Однако если ключом является последовательность символов (что чаще всего и бывает), то при применении такой функции возникает большая вероятность выработки одного и того же значения для ключей, отличающихся небольшим числом символов. Ситуацию несколько облегчает использование в качестве N простого числа. Вычисление функции становится более сложным, но вероятность выработки одного значения для разных ключей уменьшается.
Используются и более сложные способы вычисления хэш-функции основанные, например, на вырезке поднабора бит из битового представления ключа или вычислении квадратичного выражения от ORD(k). Но в любом случае с ненулевой вероятностью хэш-функция может выдать одно значение для разных значений ключа. Такая ситуация называется коллизией ключей и проявляется в том, что при попытке занести в хэш-таблицу запись с новым ключом мы наталкиваемся на то, что требуемый элемент массива уже занят. Одним из выходов (к которому рано или поздно, может быть, придется прибегнуть) является увеличение размера массива, образование новой хэш-функции и расстановка заново всех занятых элементов массива. Но поскольку возникновение коллизии может являться флуктуацией, до поры до времени обычно пытаются разрешать эту ситуацию другими способами. Традиционно принято различать методы прямой адресации (ключ, появление которого вызвало коллизию, помещается в один из свободных элементов хэш-таблицы) и методы цепочек (записи, для ключей которых выработано одинаковое значение хэш-функции связываются в линейный список).
Конструируемые типы данных
Мы переходим к рассмотрению группы разновидностей типов данных, которые в литературе часто называют "составными", поскольку любое значение любого из этих типов состоит из значений одного или нескольких других типов. Мы предпочитаем использовать термин "конструируемый тип", поскольку для каждой разновидности типов этой группы в языке программирования специфицируются средства построения (конструирования) нового типа на основе встроенных и/или ранее определенных типов, и для каждой разновидности предопределяются операции, позволяющие извлечь компонент составного значения. К наиболее распространенным конструируемым типам относятся тип массива, тип записи и тип множества.
Линейное хэширование
Идея линейного хэширования (Витольд Литвин) состоит в том, чтобы можно было обойтись без поддержания справочника в основной памяти. Основой метода является то, что для адресации блока внешней памяти всегда используются младшие биты значения хэш-функции. Если возникает потребность в расщеплении, то записи перераспределяются по блокам так, чтобы адресация осталась правильной.
Линейное зондирование
Самым простым способом разрешения коллизий является использование метода линейного зондирования (иногда его называют методом линейных проб). Идея состоит в том, что сталкиваясь с коллизией при включении записи, мы последовательно (циклически, с переходом через конец на начало) просматриваем массив в поиске первого незанятого элемента. Если такой элемент обнаруживается, в него и заносится включаемая запись (рисунок 4.18). Если все элементы массива заняты, то это означает, что хэш-таблица переполнена и требуется расширение массива и новая расстановка его элементов.

Рис. 4.18.
Если коллизия обнаруживается при поиске (т.е. следуя применяемой хэш-функции мы обращаемся по свертке ключа к элементу массива и обнаруживаем, что он занят записью с другим ключом), последовательно (циклически) просматриваются следующие элементы массива, пока не будет найдена запись с указанным ключом (рисунок 4.19), либо мы не наткнемся на свободный элемент массива. Последний вариант означает, что запись с указанным ключом в хэш-таблице отсутствует (рисунок 4.20).

Рис. 4.19.

Рис. 4.20.
Достоинством метода линейного зондирования является его очевидная простота, а недостаток состоит в том, что при разрешении коллизии вторичные элементы массива (те, на которые прямо не указывает хэш-функция) имеют обыкновение сосредотачиваться вблизи первичных элементов. Заполнение массива происходит неравномерно, и увеличивается вероятность следующих коллизий.
Массивы
Как и в ряде предыдущих разделов, понятия массива и типа массива сильно различаются в сильно и слабо типизированных языках. Начнем с классического понятия в сильно типизированных языках (например, в языке Паскаль). Тип массива в таких языках определяется на основе двух вспомогательных типов: типа элементов массива (базового типа) и типа индекса массива. В языке Паскаль определение типа массива выглядит следующим образом: type T = array [I] of T0, где T0 - базовый тип, а I - тип индекса. T0 может быть любым встроенным или ранее определенным типом. Тип индекса I должен состоять из конечного числа перечисляемых значений, т.е. быть уточненным, перечисляемым, символьным или булевским типом. В языках линии Паскаль допускается и неявное определение уточненного типа массива. Например, допустимы следующие определения типа массива: type T = array [1..6] of integer или type T = array ['a'..'e'] of real.
Если мощность множества значений типа индекса есть n, то значение типа массива - это регулярная структура, включающая n элементов базового типа. Соответствующим образом устроены и переменные типа массива. Для любого сконструированного типа массива предопределены две операции - операция конструирования значения типа массива и операция выборки элемента массива. Если x - переменная типа массива T, а i - значение соответствующего типа индекса, то для конструирования значения используется языковое средство x:= T (c1, c2, ..., cn), где c1, c2, ..., cn - значения базового типа. Для выборки элемента массива используется конструкция x[i], значением которой является значение i-того элемента массива (вместо i в квадратных скобках может содержаться любое допустимое выражение, значение которого принадлежит множеству значений типа индекса). Эта же конструкция может использоваться в левой части оператора присваивания, т.е. элементы массива могут изменяться индивидуально. Кроме того, при подобной строгой типизации массивов допустимы присваивания значений переменных типа массива, функции, возвращающие значение типа массива и т.п.
Базовым типом типа массива может быть любой встроенный или определенный тип, в том числе и тип массива.
В последнем случае говорят о многомерных массивах или матрицах. Для работы с многомерными массивами в языках используют сокращенную запись. Например, вместо определения type T = array [1..10] of array [1..5] of real можно написать type T = array [1..10],[1..5] of real, а если x - переменная такого типа T, то для выборки скалярного элемента вместо x[i][j] можно написать x[i,j]. В сильно типизированных языках для любого значения типа массива известно число элементов базового типа. Поэтому в принципе всегда возможен контроль значения индекса, хотя на практике такой контроль обычно отменяется при использовании программы в производственном режиме. Для иллюстрации приемов работы с массивами в слабо типизированных языках используем язык Си. В этом языке нет средств определения типов массива, хотя имеется возможность определения "массивных переменных". Число элементов в массивной переменной определяется либо явно, либо с помощью задания списка инициализирующих значений базового типа. Например, массивную переменную с четырьмя элементами целого типа можно определить как int x[4] (неинициализированный вариант) или как int x[] = { 0, 2, 8, 22} (инициализированная массивная переменная). Доступ к элементам массивной переменной производится с помощью конструкции выбора, по виду аналогичной соответствующей конструкции в сильно типизированных языках x[i], где i - выражение, принимающее целое значение (мы специально отметили внешний характер аналогии, поскольку в отличие от языка Паскаль в языке Си зафиксирована интерпретация операции выбора на основе более примитивных операций адресной арифметики). Однако, по причинам, которые мы обсудим в разделе, посвященном указателям, в реализациях языка Си в принципе невозможен контроль выхода значения индекса за пределы массива. Кроме того, по аналогичным причинам невозможно присваивание значений массивных переменных и не допускаются функции, вырабатывающие "массивные значения".
Методы хэширования для поиска в основной памяти
Если в предыдущем разделе речь шла о поиске необходимой информации по заданному ключу путем прямого сравнения значения аргумента с искомым ключом, то этот раздел посвящен принципиально (до некоторой степени) другому подходу к поиску. Общая идея подхода заключается в том, чтобы с помощью применения к заданному аргументу поиска x заранее определенной функции f(Ч) (хэш-функции, иногда называемой по-русски функцией расстановки) получить значение f(x), которое наилучшим образом характеризовало бы положение искомого ключа в основной или внешней памяти. В этом разделе мы сосредоточимся на такого рода методах поиска данных в основной памяти.
Замечание по поводу терминологии. В течение многих лет в сообществе российских программистов обсуждался вопрос применения русскоязычной терминологии, относящейся к хэшированию. Кроме упомянутого выше термина "расстановка", предлагалось использовать "русский" термин "рандомизация". Поскольку, как видно, для этого подхода нет подходящего названия на русском языке, мы будем использовать транслитерацию английского термина "hashing" - хэширование.
Методы хэширования для поиска во внешней памяти
Идея доступа к данным на основе хэширования настолько привлекательна (потенциальная возможность за одно обращение к памяти получить требуемые данные), что от нее невозможно отказаться при работе с данными во внешней памяти. Исходная идея кажется очевидной: если при управлении данными на основе хэширования в основной памяти хэш-функция вырабатывает адрес требуемого элемента, то при обращении к внешней памяти необходимо генерировать номер блока дискового пространства, в котором находится запрашиваемый элемент данных. Основная проблема относится к коллизиям. Если при работе в основной памяти потенциально возникающими потребностями дополнительного поиска информации при возникновении коллизий можно, вообще говоря, пренебречь (поскольку время доступа к основной памяти мало), то при использовании внешней памяти любое дополнительное обращение вызывает существенные накладные расходы. Основные методы хэширования для поиска информации во внешней памяти направлены на решение именно этой задачи. Заметим, что автором и первооткрывателем большинства идей хэширования во внешней памяти является Витольд Литвин.
Методы поиска в основной памяти
В этой части книги будут обсуждаться структуры данных в основной памяти и методы их использования, предназначенные для поиска данных в соответствии со значениями их ключей. Эта задача является не менее распространенной в программировании, чем внутренняя сортировка данных.
Главным образом, распространены два подхода - поиск в динамических древовидных структурах и поиск в таблицах на основе хэширования. Рассмотрению разновидностей этих подходов и посвящены следующие два раздела.
Заметим, что мы намеренно выделили в отдельную часть структуры данных и методы поиска данных во внешней памяти. Несмотря на использование того же набора терминов (деревья и хэширование) поиск во внешней памяти и критерии оценки эффективности алгоритмов существенно отличаются от тех, которые применимы в случае расположения данных в основной памяти.
Методы поиска в основной памяти на основе деревьев
Понятия, связанные с деревьями, широко известны и интуитивно понятны. Тем не менее, для однозначного понимания содержимого этого раздела (и соответствующего раздела следующей части курса) мы приведем несколько не слишком формальных определений и примеров.
Существует несколько возможных определений дерева. Например, с точки зрения теории графов деревом часто называют неориентированный граф с выделенной вершиной (корнем), который не содержит циклов. Нас будут интересовать не произвольные графы, а только ориентированные деревья, причем с точки зрения программистов. Поэтому мы используем следующее рекурсивное определение: дерево R с базовым типом T - это либо (a) пустое дерево (не содержащее ни одной вершины), либо (b) некоторая вершина типа T (корень дерева) с конечным (возможно, нулевым) числом связанных с ней деревьев с базовым типом T (эти деревья называются поддеревьями дерева R). Из этого определения, в частности, следует, что однонаправленный список (рисунок 4.1) является деревом.

Рис. 4.1.
Деревья можно представлять по-разному (это всего лишь однородная иерархическая структура). Например, на рисунках 4.1 и 4.2 показаны два разных способа представления одного и того же дерева, у которого базовый тип содержит множество букв латинского алфавита. Сразу заметим, что графовое представление на рисунке 4.2 больше соответствует специфике программирования.

Рис.4.2.
Придерживаясь естественной для графового представления терминологии, мы будем называть связи между поддеревьями ветвями, а корень каждого поддерева - вершиной. Упорядоченным деревом называется такое, у которого ветви, исходящие из каждой вершины, упорядочены. Например, два упорядоченных дерева на рисунке 4.3 различаются.

Рис.4.3.
По определению, корень дерева находится на уровне 0, а все вершины дерева, непосредственно связанные с вершиной уровня i, находятся на уровне i+1. Вершина x уровня i, непосредственно связанная с вершиной y уровня i+1, называется непосредственным предком (или родителем) вершины y. Такая вершина y соответственно называется непосредственным потомком (или сыном) вершины x. Вершина без непосредственных потомков называется листовой (или терминальной), нелистовые вершины называются внутренними. Под степенью внутренней вершины понимается число ее непосредственных потомков. Если все вершины имеют одну и ту же степень, то она полагается степенью дерева. На самом деле, всегда можно добиться того, чтобы любая вершина дерева имела одну и ту же степень путем добавления специальных вершин в тех точках, где отсутствуют поддеревья (рисунок 4.4).
Число вершин (или ветвей), которые нужно пройти от корня к вершине x, называется длиной пути к вершине x. Высотой (или глубиной) дерева будем называть максимальную длину его вершины.

Рис. 4.4.
Методы поиска во внешней памяти
Как и в случае необходимости сортировки данных, не размещаемых целиком в основной памяти, для поиска данных во внешней памяти существует ряд методов, несколько напоминающих те, которые упоминались в предыдущей части, но сильно отличающихся по своей сути. Эти методы по названиям похожи на те, которые используются для поиска данных в основной памяти - деревья и хэширование, - но устроены совсем другим образом, чтобы минимизировать число обращений к внешней памяти.
Методы поиска во внешней памяти на основе деревьев
Базовым "древовидным" аппаратом для поиска данных во внешней памяти являются B-деревья. В основе этого механизма лежат следующие идеи. Во-первых, поскольку речь идет о структурах данных во внешней памяти, общее время доступа к которой определяется в основном не объемом последовательно расположенных данных, а временем подвода магнитных головок (см. введение в Часть 3), то выгодно получать за одно обращение к внешней памяти как можно больше информации, учитывая при этом необходимость экономного использования основной памяти. При сложившемся подходе к организации основной памяти в виде набора страниц равного размера естественно считать именно страницу единицей обмена с внешней памятью. Во-вторых, желательно обеспечить такую поисковую структуру во внешней памяти, при использовании которой поиск информации по любому ключу требует заранее известного числа обменов с внешней памятью.
Методы внешней сортировки
Принято называть "внешней" сортировкой сортировку последовательных файлов, располагающихся во внешней памяти и слишком больших, чтобы можно было целиком переместить их в основную память и применить один из рассмотренных в предыдущем разделе методов внутренней сортировки. Наиболее часто внешняя сортировка применяется в системах управления базами данных при выполнении запросов, и от эффективности применяемых методов существенно зависит производительность СУБД.
Следует пояснить, почему речь идет именно о последовательных файлах, т.е. о файлах, которые можно читать запись за записью в последовательном режиме, а писать можно только после последней записи. Методы внешней сортировки появились, когда наиболее распространенными устройствами внешней памяти были магнитные ленты. Для лент чисто последовательный доступ был абсолютно естественным. Когда произошел переход к запоминающим устройствам с магнитными дисками, обеспечивающими "прямой" доступ к любому блоку информации, казалось, что чисто последовательные файлы потеряли свою актуальность. Однако это ощущение было ошибочным.
Все дело в том, что практически все используемые в настоящее время дисковые устройства снабжены подвижными магнитными головками. При выполнении обмена с дисковым накопителем выполняется подвод головок к нужному цилиндру, выбор нужной головки (дорожки), прокрутка дискового пакета до начала требуемого блока и, наконец, чтение или запись блока. Среди всех этих действий самое большое время занимает подвод головок. Именно это время определяет общее время выполнения операции. Единственным доступным приемом оптимизации доступа к магнитным дискам является как можно более "близкое" расположение на накопителе последовательно адресуемых блоков файла. Но и в этом случае движение головок будет минимизировано только в том случае, когда файл читается или пишется в чисто последовательном режиме. Именно с такими файлами при потребности сортировки работают современные СУБД.
Следует также заметить, что на самом деле скорость выполнения внешней сортировки зависит от размера буфера (или буферов) основной памяти, которая может быть использована для этих целей. Мы остановимся на этом в конце этой части книги. Сначала же мы рассмотрим основные методы внешней сортировки, работающие при минимальных расходах основной памяти.
Методы внутренней сортировки
В этой и следующей частях книги мы будем обсуждать методы сортировки информации. В общей постановке задача ставится следующим образом. Имеется последовательность однотипных записей, одно из полей которых выбрано в качестве ключевого (далее мы будем называть его ключом сортировки). Тип данных ключа должен включать операции сравнения ("=", ">", "<", ">=" и "<="). Задачей сортировки является преобразование исходной последовательности в последовательность, содержащую те же записи, но в порядке возрастания (или убывания) значений ключа. Метод сортировки называется устойчивым, если при его применении не изменяется относительное положение записей с равными значениями ключа.
Различают сортировку массивов записей, целиком расположенных в основной памяти (внутреннюю сортировку), и сортировку файлов, хранящихся во внешней памяти и не помещающихся полностью в основной памяти (внешнюю сортировку). Для внутренней и внешней сортировки требуются существенно разные методы. В этой части мы рассмотрим наиболее известные методы внутренней сортировки, начиная с простых и понятных, но не слишком быстрых, и заканчивая не столь просто понимаемыми усложненными методами.
Естественным условием, предъявляемым к любому методу внутренней сортировки является то, что эти методы не должны требовать дополнительной памяти: все перестановки с целью упорядочения элементов массива должны производиться в пределах того же массива. Мерой эффективности алгоритма внутренней сортировки являются число требуемых сравнений значений ключа (C) и число перестановок элементов (M).
Заметим, что поскольку сортировка основана только на значениях ключа и никак не затрагивает оставшиеся поля записей, можно говорить о сортировке массивов ключей. В следующих разделах, чтобы не привязываться к конкретному языку программирования и его синтаксическим особенностям, мы будем описывать алгоритмы словами и иллюстрировать их на простых примерах.
Многофазная сортировка
При использовании рассмотренного выше метода сбалансированной многопутевой внешней сортировки на каждом шаге примерно половина вспомогательных файлов используется для ввода данных и примерно столько же для вывода сливаемых серий. Идея многофазной сортировки состоит в том, что из имеющихся m вспомогательных файлов (m-1) файл служит для ввода сливаемых последовательностей, а один - для вывода образуемых серий. Как только один из файлов ввода становится пустым, его начинают использовать для вывода серий, получаемых при слиянии серий нового набора (m-1) файлов. Таким образом, имеется первый шаг, при котором серии исходного файла распределяются по m-1 вспомогательному файлу, а затем выполняется многопутевое слияние серий из (m-1) файла, пока в одном из них не образуется одна серия.
Очевидно, что при произвольном начальном распределении серий по вспомогательным файлам алгоритм может не сойтись, поскольку в единственном непустом файле будет существовать более, чем одна серия. Предположим, например, что используется три файла B1, B2 и B3, и при начальном распределении в файл B1 помещены 10 серий, а в файл B2 - 6. При слиянии B1 и B2 к моменту, когда мы дойдем до конца B2, в B1 останутся 4 серии, а в B3 попадут 6 серий. Продолжится слияние B1 и B3, и при завершении просмотра B1 в B2 будут содержаться 4 серии, а в B3 останутся 2 серии. После слияния B2 и B3 в каждом из файлов B1 и B2 будет содержаться по 2 серии, которые будут слиты и образуют 2 серии в B3 при том, что B1 и B2 - пусты. Тем самым, алгоритм не сошелся (таблица 3.2).
Таблица 3.2. Пример начального распределения серий, при котором трехфазная внешняя сортировка не приводит к нужному результату
| Число серий в файле B1 | Число серий в файле B2 | Число серий в файле B3 |
| 10 | 6 | 0 |
| 4 | 0 | 6 |
| 0 | 4 | 2 |
| 2 | 2 | 0 |
| 0 | 0 | 2 |
Попробуем понять, каким должно быть начальное распределение серий, чтобы алгоритм трехфазной сортировки благополучно завершал работу и выполнялся максимально эффективно. Для этого рассмотрим работу алгоритма в обратном порядке, начиная от желательного конечного состояния вспомогательных файлов.
Нас устраивает любая комбинация конечного числа серий в файлах B1, B2 и B3 из (1,0,0), (0,1,0) и (0,0,1). Для определенности выберем первую комбинацию. Для того, чтобы она сложилась, необходимо, чтобы на непосредственно предыдущем этапе слияний существовало распределение серий (0,1,1). Чтобы получить такое распределение, необходимо, чтобы на непосредственно предыдущем этапе слияний распределение выглядело как (1,2,0) или (1,0,2). Опять для определенности остановимся на первом варианте. Чтобы его получить, на предыдущем этапе годились бы следующие распределения: (3,0,2) и (0,3,1). Но второй вариант хуже, поскольку он приводится к слиянию только одной серии из файлов B2 и B3, в то время как при наличии первого варианта распределения будут слиты две серии из файлов B1 и B3. Пожеланием к предыдущему этапу было бы наличие распределения (0,3,5), еще раньше - (5,0,8), еще раньше - (13,8,0) и т.д. Это рассмотрение показывает, что метод трехфазной внешней сортировки дает желаемый результат и работает максимально эффективно (на каждом этапе сливается максимальное число серий), если начальное распределение серий между вспомогательными файлами описывается соседними числами Фибоначчи. Напомним, что последовательность чисел Фибоначчи начинается с 0, 1, а каждое следующее число образуется как сумма двух предыдущих: (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ....) Аналогичные (хотя и более громоздкие) рассуждения показывают, что в общем виде при использовании m вспомогательных файлов условием успешного завершения и эффективной работы метода многофазной внешней сортировки является то, чтобы начальное распределение серий между m-1 файлами описывалось суммами соседних (m-1), (m-2), ..., 1 чисел Фибоначчи порядка m-2. Последовательность чисел Фибоначчи порядка p начинается с p нулей, (p+1)-й элемент равен 1, а каждый следующий равняется сумме предыдущих p+1 элементов. Ниже показано начало последовательности чисел Фибоначчи порядка 4: (0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 31, 61, ...) При использовании шести вспомогательных файлов идеальными распределениями серий являются следующие:
1 0 0 0 0 1 1 1 1 1 2 2 2 2 1 4 4 4 3 2 8 8 7 6 4 16 15 14 12 8 ........
Понятно, что если распределение основано на числе Фибоначчи fi, то минимальное число серий во вспомогательных файлах будет равно fi, а максимальное - f(i+1). Поэтому после выполнения слияния мы получим максимальное число серий - fi, а минимальное - f(i-1). На каждом этапе будет выполняться максимально возможное число слияний, и процесс сойдется к наличию всего одной серии. Поскольку число серий в исходном файле может не обеспечивать возможность такого распределения серий, применяется метод добавления пустых серий, которые в дальнейшем как можно более равномерного распределяются между промежуточными файлами и опознаются при последующих слияниях. Понятно, что чем меньше таких пустых серий, т.е. чем ближе число начальных серий к требованиям Фибоначчи, тем более эффективно работает алгоритм.
Множества
Еще одной разновидностью конструируемых типов являются типы множеств. Такие типы поддерживаются только в развитых сильно типизированных языках. В языке Паскаль тип множества определяется конструкцией type T = set of T0, где T0 - встроенный или ранее определенный тип данных (базовый тип). Значениями переменных типа T являются множества элементов типа T0 (в частности, пустые множества).
Для любого типа множества определены следующие операции: "?" - пересечение множеств, "+" - объединение множеств, "-" - вычитание множеств и "in" - проверка принадлежности к множеству элемента базового типа.
С использованием механизма множеств можно писать лаконичные и красивые программы, но нужно отдавать себе отчет в том, что для эффективной реализации множеств требуются серьезные ограничения их мощности. Обычно в реализациях языков допускаются множества, мощность базового типа которых не превосходит длину машинного слова. Это связано с тем, что перечисленные выше операции допускают эффективную реализацию только в том случае, когда значение множества представляется битовой шкалой, длина которой равна мощности базового типа. "1" означает, что соответствующий элемент базового типа входит в множество, "0" - не входит. Чтобы для выполнения операций над множествами можно было прямо использовать машинные команды, нужно ограничить длину шкалы машинным словом.
Наследование таблиц и семантика включения
Если таблица определена на одном строчном типе (без добавления столбцов), то разрешается использовать ее как супертаблицу и производить на ее основе подтаблицы с добавлением столбцов. При этом используется семантика включения.
Считается, что любая супертаблица включает строки всех своих подтаблиц, спроецированных на заголовок супертаблицы (кроме того, при работе с супертаблицей можно явно указать, что пользователя или прикладную программу интересуют только "собственные" строки супертаблицы). В ряде случаев использование механизма наследования таблиц с использованием семантики включения позволяет более правильно (без излишеств) спроектировать базу данных и обойтись без привлечения операторов объединения при формулировке сводных запросов.
Наследование типов
Под наследованием типов понимается возможность дисциплинированного создания новых типов на основе уже определенных. Мы подчеркиваем слово "дисциплинированного", потому что, конечно, можно определять новые типы и произвольным образом, используя в качестве заготовок куски существующих программных текстов.
В отличие от этого, при использовании механизма наследования типов требуется, чтобы спецификация нового типа (подтипа) полностью включала спецификацию наследуемого типа (супертипа). Но эта спецификация может быть расширена сигнатурами дополнительных операций, вводимых для подтипа. Соответственно в реализации подтипа должны присутствовать коды функций и/или процедур дополнительных операций, а структуры данных, функции и процедуры супертипа могут быть переопределены.
В разных языках с абстрактными типами данных допускается либо только простое наследование типов (для каждого подтипа существует только один супертип), либо множественное наследование (для подтипа может существовать несколько супертипов). Множественное наследование порождает проблему согласования сигнатур операций супертипов. Общего решения этой проблемы не существует, в каждом из языков с множественным наследованием используются свои приемы. Мы не будем более подробно останавливаться на этих деталях.
Имеются два основных соображения по поводу пользы механизма наследования типов. Во-первых, этот механизм обеспечивает возможность контролируемого и дисциплинированного повторного использования программных кодов. Во-вторых (и может быть, это даже более важно), во многих языках используется так называемая семантика включения: считается, что значение любого подтипа одновременно является значением любого своего супертипа. Семантика включения хорошо соответствует смыслу механизма наследования как средства уточненной классификации объектов предметной области.
На рисунке 1.5 показана простая схема образования типов на основе одиночного наследования. Естественно, что в подтипах типа "Человек" появляются дополнительные операции, например, "размер пособия" для безработных и "должностной оклад" для служащих.
Можно предположить, что операция "знание языков", вводимая для типа "Служащий", по- разному переопределяется для его подтипов "Программист" и "Преподаватель".
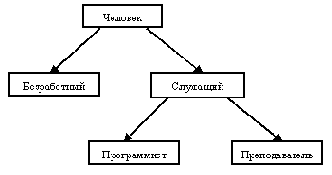
Рис. 1.5. С другой стороны, очевидно, что из соображений здравого смысла и безработные, и служащие обладают общими свойствами, характерными для типа "Человек", а программисты и преподаватели относятся к категории "Служащие". Эти соображения приводят нас к рисунку 1.6, на котором показана иерархия включения значений этих типов данных. Это означает, что, в частности, должна иметься возможность единообразной работы со значениями типа "Человек" независимо от того, сформировано ли соответствующее значение конструктором этого типа или же конструктором любого из его подтипов. Конечно, при этом можно использовать только те операции, которые специфицированы во внешнем представлении типа "Человек".
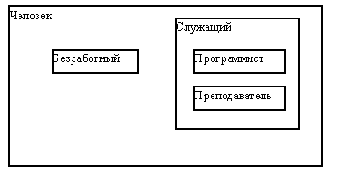
Рис. 1.6. Поскольку в подтипе может быть переопределена реализация операций, специфицированных в супертипе, то во время компиляции программы иногда невозможно установить, какую функцию или процедуру требуется вызывать при выполнении операции над значением типа. По этой причине в системах программирования, поддерживающих развитый механизм наследования, для обеспечения корректного вызова функций и/или процедур, которые реализуют операции типа, приходится применять так называемый метод позднего связывания (late binding). Суть этого метода состоит в том, что во время выполнения программы при каждом значении (или объекте в языках объектно-ориентированного программирования) содержится информация о типе, с помощью конструктора которого было создано это значение. На основе этой информации на стадии выполнения удается обнаружить требуемые реализации операций. Понятно, что применение метода позднего связывания вносит в процесс выполнения программы существенный элемент интерпретации, что приводит к снижению эффективности. Поэтому, по мере возможности, стремятся снизить накладные расходы даже за счет понижения универсальности механизма наследования.Примером может служить аппарат виртуальных функций в языке Си++.
Объектные типы данных
Эта разновидность типов ближе всего к абстрактным типам данных в языках программирования. Идея состоит в том, что сначала специфицируется определяемый пользователем тип данных (переименовывается некоторый встроенный тип, определяется строчный тип или тип коллекции). Затем для этого типа можно специфицировать (конечно, предварительно написав соответствующие программы) ряд определяемых пользователем функций. Строго говоря, после этого можно считать, что тип инкапсулирован этим набором функций, хотя не все разработчики считают строгую инкапсуляцию необходимой.
После полной спецификации объектного типа его можно использовать как встроенный или любой ранее определенный тип. Видимо, в будущих реализациях объектно-реляционных СУБД появится и полная возможность наследования объектных типов.
Обменная сортировка
Простая обменная сортировка (в просторечии называемая "методом пузырька") для массива a[1], a[2], ..., a[n] работает следующим образом. Начиная с конца массива сравниваются два соседних элемента (a[n] и a[n-1]). Если выполняется условие a[n-1] > a[n], то значения элементов меняются местами. Процесс продолжается для a[n-1] и a[n-2] и т.д., пока не будет произведено сравнение a[2] и a[1]. Понятно, что после этого на месте a[1] окажется элемент массива с наименьшим значением. На втором шаге процесс повторяется, но последними сравниваются a[3] и a[2]. И так далее. На последнем шаге будут сравниваться только текущие значения a[n] и a[n-1]. Понятна аналогия с пузырьком, поскольку наименьшие элементы (самые "легкие") постепенно "всплывают" к верхней границе массива. Пример сортировки методом пузырька показан в таблице 2.3.
Таблица 2.3. Пример сортировки методом пузырька
| Начальное состояние массива | 8 23 5 65 44 33 1 6 |
| Шаг 1 | 8 23 5 65 44 33 1 6 8 23 5 65 44 1 33 6 8 23 5 65 1 44 33 6 8 23 5 1 65 44 33 6 8 23 1 5 65 44 33 6 8 1 23 5 65 44 33 6 1 8 23 5 65 44 33 6 |
| Шаг 2 | 1 8 23 5 65 44 6 33 1 8 23 5 65 6 44 33 1 8 23 5 6 65 44 33 1 8 23 5 6 65 44 33 1 8 5 23 6 65 44 33 1 5 8 23 6 65 44 33 |
| Шаг 3 | 1 5 8 23 6 65 33 44 1 5 8 23 6 33 65 44 1 5 8 23 6 33 65 44 1 5 8 6 23 33 65 44 1 5 6 8 23 33 65 44 |
| Шаг 4 | 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 |
| Шаг 5 | 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 |
| Шаг 6 | 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 |
| Шаг 7 | 1 5 6 8 23 33 44 65 |
Для метода простой обменной сортировки требуется число сравнений nx(n-1)/2, минимальное число пересылок 0, а среднее и максимальное число пересылок - O(n2).
Метод пузырька допускает три простых усовершенствования. Во-первых, как показывает таблица 2.3, на четырех последних шагах расположение значений элементов не менялось (массив оказался уже упорядоченным). Поэтому, если на некотором шаге не было произведено ни одного обмена, то выполнение алгоритма можно прекращать.
Во-вторых, можно запоминать наименьшее значение индекса массива, для которого на текущем шаге выполнялись перестановки. Очевидно, что верхняя часть массива до элемента с этим индексом уже отсортирована, и на следующем шаге можно прекращать сравнения значений соседних элементов при достижении такого значения индекса. В-третьих, метод пузырька работает неравноправно для "легких" и "тяжелых" значений. Легкое значение попадает на нужное место за один шаг, а тяжелое на каждом шаге опускается по направлению к нужному месту на одну позицию. На этих наблюдениях основан метод шейкерной сортировки (ShakerSort). При его применении на каждом следующем шаге меняется направление последовательного просмотра. В результате на одном шаге "всплывает" очередной наиболее легкий элемент, а на другом "тонет" очередной самый тяжелый. Пример шейкерной сортировки приведен в таблице 2.4.
Таблица 2.4. Пример шейкерной сортировки
| Начальное состояние массива | 8 23 5 65 44 33 1 6 |
| Шаг 1 | 8 23 5 65 44 33 1 6 8 23 5 65 44 1 33 6 8 23 5 65 1 44 33 6 8 23 5 1 65 44 33 6 8 23 1 5 65 44 33 6 8 1 23 5 65 44 33 6 1 8 23 5 65 44 33 6 |
| Шаг 2 | 1 8 23 5 65 44 33 6 1 8 5 23 65 44 33 6 1 8 5 23 65 44 33 6 1 8 5 23 44 65 33 6 1 8 5 23 44 33 65 6 1 8 5 23 44 33 6 65 |
| Шаг 3 | 1 8 5 23 44 6 33 65 1 8 5 23 6 44 33 65 1 8 5 6 23 44 33 65 1 8 5 6 23 44 33 65 1 5 8 6 23 44 33 65 |
| Шаг 4 | 1 5 6 8 23 44 33 65 1 5 6 8 23 44 33 65 1 5 6 8 23 44 33 65 1 5 6 8 23 33 44 65 |
| Шаг 5 | 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 |
Перечисляемые типы данных
Перечисляемый тип состоит из конечного числа упорядоченных именованных значений. В классическом варианте, свойственном, например, языкам линии Паскаль, определение типа состоит из перечисления имен значений (поэтому справедливо называть такой тип перечисляемым), эти имена в дальнейшем играют роль имен литеральных констант этого типа и должны отличаться от литерального изображения констант любого другого типа. Поскольку значения типа задаются путем перечисления, каждому значению можно однозначно сопоставить натуральное число от 1 до n, где n - число значений перечисляемого типа.
Обычно для любого перечисляемого типа предопределяются операции получения значения по его номеру и получения номера по значению. Кроме того, для перечисляемого типа предопределяются операции сравнения и получения следующего и предыдущего значения. По причине однозначного сопоставления значению перечисляемого типа натурального числа, возможно неявное преобразование этих значений к значению любого числового типа данных.
В языках линии Си под тем же термином "перечисляемый тип" понимается нечто другое, поскольку при определении такого типа можно явно сопоставить имени значения некоторое целое (не обязательно положительное) число; при отсутствии явного задания целого первому элементу перечисляемого типа неявно соответствует 0, а каждому следующему - целое значение, на единицу большее целого значения предыдущего элемента. При этом (a) использование имени перечисляемого типа для объявления переменной эквивалентно использованию типа integer, и такая переменная может содержать любое целое значение; (b) имена значений перечисляемого типа на самом деле понимаются как имена целых констант, и к этим значениям применимы все операции над целыми числами, даже если они выводят за пределы множества целых значений элементов перечисляемого типа. Так что перечисляемый тип в смысле языка Си - это не совсем тип в строгом смысле этого слова, а скорее удобное задание группы именованных констант целого типа.
Понятие типа данных
Существует много подходов к определению понятия типа данных от полностью математических, основанных на аппаратах абстрактной алгебры или математической логики, до полностью житейских, ориентированных исключительно на интуицию. Автору книги ближе всего подход, применяемый классиком компьютерной литературы и создателем ряда исключительно стройных и красивых языков программирования Никласом Виртом.
Основным принципом типизации, принятым в языках программирования и базах данных является то, что любая константа, переменная, выражение и функция относится к некоторому типу, характеризующему прежде всего множество значений, к которым относятся константы, которые могут принимать переменные и выражения и которые могут формировать функции. При описании любых используемых констант, переменных и функций явно или неявно указывается их тип. В первую очередь это дает возможность компилятору и/или системе управления базами данных выделить для хранения объекта данных ровно тот объем памяти, который определяется допустимым диапазоном значений типа. Однако концепция типа этим не исчерпывается.
Следующим исключительно важным свойством типа данных является инкапсуляция внутреннего представления его значений. К значению типа данных (значения констант, переменных, выражений и функций) можно обращаться только с помощью операций, предопределенных в описании этого типа. Эти операции могут быть явными (например, арифметические операции "+", "-", "?" и "/" для числовых типов) или неявными (например, операция преобразования значения целого типа к значению плавающего типа; заметим, что в некоторых языках, в частности, в Си и Си++, допускаются и явные преобразования типов).
Наличие типовых описаний констант, переменных и функций и предписанные правила определения типов выражений вместе с поддержкой свойства инкапсуляции типов дают возможность компиляторам языков программирования и языков баз данных производить существенный контроль допустимости языковых конструкций на этапе компиляции, что позволяет сократить число проверок на стадии выполнения программ и облегчить их отладку.
Один из характерных примеров преимущества использования типизированных языков программирования представляет история операционной системы UNIX.
Как известно, система первоначально была написана на языке ассемблера PDP-7. При переходе к использованию PDP-11 ОС UNIX была переписана на языке более высокого уровня B, который являлся прямым наследником безтипового языка программирования BCPL. В очень скором времени по мере роста размеров системы ее разработчикам стало понятно, что бесчисленные проверки времени выполнения очень усложняют отладку и замедляют работу системы. Это явилось исходным толчком к внедрению в язык B системы типов и созданию типизированного языка Си, опора на который обеспечила более чем 25-летнюю плодотворную жизнь системы. Можно приводить различные классификации типов данных, например, простые и составные типы, предопределенные и определяемые типы и т.д. Существенно то, что несмотря на многолетнее использование типов данных в отечественном программировании, так и не сложилась устойчивая и общепринятая русскоязычная терминология. Поэтому в этой книге будем использовать некоторый набор терминов, выбранных из соображений максимальной распространенности и интуитивной ясности. Выделим следующие категории типов:
Встроенные типы данных, т.е. типы, предопределенные в языке программирования или языке баз данных. Обычно в языке фиксируются внешнее представление значений этих типов (вид литеральных констант) и набор операций с описанием их семантики. Внутреннее представление и реализация операций выбираются в конкретных компиляторах и подсистемах поддержки выполнения программ. Под термином "уточняемый тип данных" мы понимаем возможность определения типа на основе встроенного типа данных, значения которого упорядочены. В частности, к категории уточняемых типов относится тип поддиапазона целых чисел в языках линии Паскаль. Категорию перечисляемых типов данных составляют явно определяемые целые типы с конечным числом именованных значений. Это очень простой и легко реализуемый механизм, часто являющийся очень полезным.
Замечание: использование уточняемых и перечисляемых типов порождает потребность в динамической проверке корректности значений - выхода значения за пределы явно (в случае уточняемых типов) или неявно (в случае перечисляемых типов) диапазона. Конструируемые типы (иногда их называют составными) обладают той особенностью, что в языке предопределены средства спецификации таких типов и некоторый набор операций, дающих возможность доступа к компонентам составных значений.
Мы обсудим наиболее распространенные разновидности конструируемых типов: типы массивов, записей и множеств, а также различия в понимании этих типов в разных языках.
Замечание: будучи согласны с переводчиком книги Никласа Вирта Д.Б.Подшиваловым в том, что русские термины "тип массива", "тип записи", "тип множества" и т.д. не совсем соответствуют английским оригиналам "array type", "record type", "set type" и т.д. мы все же не будем использовать рекомендуемые им термины "записной тип", "массивный тип" и "множественный тип", поскольку (a) они тоже не вполне соответствуют оригинальным терминам и (b) ужасно выглядят и произносятся. Указательные типы дают возможность работы с типизированными множествами абстрактных адресов переменных, содержащих значения некоторого типа. В сильно типизированных языках (Паскаль, Модула, Ада и т.д.) работа с указателями сильно ограничена. В частности, невозможно получить значение указателя явно определенной переменной и/или применять к известным значениям указателей адресную арифметику. В языках с более слабой типизацией (например, Си/Си++) допускаются практически неограниченные манипуляции указателями. Вообще говоря, упоминавшиеся выше уточняемые, перечисляемые и конструируемые типы данных являются типами, определяемыми пользователями. Но эти определения не могут включать спецификацию операций над значениями типов. Допустимые операции либо предопределены, либо наследуются от некоторого определенного ранее или встроенного типа. Под термином "определяемый пользователем тип данных" (ранее был больше распространен термин "абстрактный тип данных", однако мы не будем здесь его использовать, поскольку, на наш взгляд, он не точно отражает смысл понятия) мы будем понимать возможность полного определения нового типа, включая явную или неявную спецификацию множества значений, спецификацию внутреннего представления значений типа и спецификацию набора операций над значениями определяемого типа.
Наконец, под термином "полнотиповая система" мы понимаем систему типов, в которых типы, определяемые пользователем, равноправны с предопределенными типами, т.е.можно, например, определить тип массива с элементами любого определенного типа, можно использовать определяемый пользователем тип на основе любого определенного типа и т.д.
Представление типа
При программировании с использованием АТД возможны три подхода (они могут быть смешаны): (1) перед началом написания основной программы полностью определить все требуемые типы данных; (2) определить только те характеристики АТД, которые требуются для написания программы и проверки ее синтаксической корректности; (3) воспользоваться готовыми библиотечными определениями. В каждом из этих подходов имеются свои достоинства и недостатки, но их объединяет то, что при написании программы известны по меньшей мере внешние характеристики всех типов данных. В некотором смысле это означает, что расширен язык программирования.
Подобная внешняя характеристика АТД называется его представлением или спецификацией. Представление включает имя АТД и набор спецификаций доступных пользователю операций со значениями этого типа. Со своей стороны, спецификация операции состоит из имени и типов параметров (в последнее время такие спецификации принято называть сигнатурами операций). Для однозначного определения компилятором того, какая реально функция или процедура должна быть вызвана при обращении к операции, обычно требуют, чтобы сигнатуры всех операций всех АТД, используемых в программе, были различны (мы еще вернемся к этой теме ниже при обсуждении возможностей полиморфизма).
Переменные, используемые для внутреннего представления значений типа называются переменными состояния, а их совокупность состоянием значений.
Иногда исходя из соображений эффективности допускается прямой доступ к некоторым переменным состояния значений типа (путем использования обычных предопределенных операций чтения и записи). В этом случае переменные состояния, доступные в таком режиме, также специфицируются во внешнем представлении типа.
Прямое слияние
Начнем с того, как можно использовать в качестве метода внешней сортировки алгоритм простого слияния, обсуждавшийся в конце предыдущей части. Предположим, что имеется последовательный файл A, состоящий из записей a1, a2, ..., an (снова для простоты предположим, что n представляет собой степень числа 2). Будем считать, что каждая запись состоит ровно из одного элемента, представляющего собой ключ сортировки. Для сортировки используются два вспомогательных файла B и C (размер каждого из них будет n/2).
Сортировка состоит из последовательности шагов, в каждом из которых выполняется распределение состояния файла A в файлы B и C, а затем слияние файлов B и C в файл A. (Заметим, что процедура слияния для файлов полностью иллюстрируется рисунком 2.14.) На первом шаге для распределения последовательно читается файл A, и записи a1, a3, ..., a(n-1) пишутся в файл B, а записи a2, a4, ..., an - в файл C (начальное распределение). Начальное слияние производится над парами (a1, a2), (a3, a4), ..., (a(n-1), an), и результат записывается в файл A. На втором шаге снова последовательно читается файл A, и в файл B записываются последовательные пары с нечетными номерами, а в файл C - с четными. При слиянии образуются и пишутся в файл A упорядоченные четверки записей. И так далее. Перед выполнением последнего шага файл A будет содержать две упорядоченные подпоследовательности размером n/2 каждая. При распределении первая из них попадет в файл B, а вторая - в файл C. После слияния файл A будет содержать полностью упорядоченную последовательность записей. В таблице 3.1 показан пример внешней сортировки простым слиянием.
Таблица 3.1. Пример внешней сортировки прямым слиянием
| Начальное состояние файла A | 8 23 5 65 44 33 1 6 |
|
Первый шаг Распределение Файл B Файл C Слияние: файл A |
8 5 44 1 23 65 33 6 8 23 5 65 33 44 1 6 |
|
Второй шаг Распределение Файл B Файл C Слияние: файл A |
8 23 33 44 5 65 1 6 5 8 23 65 1 6 33 44 |
|
Третий шаг Распределение Файл B Файл C Слияние: файл A |
5 8 23 65 1 6 33 44 1 5 6 8 23 33 44 65 |
Заметим, что для выполнения внешней сортировки методом прямого слияния в основной памяти требуется расположить всего лишь две переменные - для размещения очередных записей из файлов B и C. Файлы A, B и C будут O(log n) раз прочитаны и столько же раз записаны.
R-деревья и их использование для организации индексов в пространственных базах данных
Коротко рассмотрим еще одно расширение механизма B-деревьев, используемое главным образом для организации индексов в пространственных базах данных, - R-деревья. Подобно B+-деревьям, R-дерево представляет собой ветвистую сбалансированную древовидную структуру с разной организацией внутренних и листовых страниц.
Но информация, хранящаяся в R-дереве несколько отличается от той, которая содержится в B-деревьях. В дополнение к находящимся в листовых страницах идентификаторам пространственных объектов, в R-деревьях хранится информация о границах индексируемого объекта. В случае двумерного пространства сохраняются горизонтальные и вертикальные координаты нижнего левого и верхнего правого углов наименьшего прямоугольника, содержащего индексируемый объект. Пример простого R-дерева, содержащего информацию о шести пространственных объектах, приведен на рисунке 5.7.

Рис. 5.7. Простое R-дерево для представления шести пространственных объектов
Расширяемое хэширование
В основе подхода расширяемого хэширования (Extendible Hashing) лежит принцип использования деревьев цифрового поиска в основной памяти. В основной памяти поддерживается справочник, организованный на основе бинарного дерева цифрового поиска, ключами которого являются значения хэш-функции, а в листовых вершинах хранятся номера блоков записей во внешней памяти. В этом случае любой поиск в дереве цифрового поиска является "успешным", т.е. ведет к некоторому блоку внешней памяти. Входит ли в этот блок искомая запись, обнаруживается уже после прочтения блока в основную память.
Проблема коллизий переформулируется следующим образом. Как таковых, коллизий не существует. Может возникнуть лишь ситуация переполнения блока внешней памяти. Значение хэш-функции указывает на этот блок, но места для включения записи в нем уже нет. Эта ситуация обрабатывается так. Блок расщепляется на два, и дерево цифрового поиска переформируется соответствующим образом. Конечно, при этом может потребоваться расширение самого справочника.
Расширяемое хэширование хорошо работает в условиях динамически изменяемого набора записей в хранимом файле, но требует наличия в основной памяти справочного дерева.
Разновидности B+-деревьев для организации индексов в базах данных
B+-деревья наиболее интенсивно используются для организации индексов в базах данных. В основном это определяется двумя свойствами этих деревьев: предсказуемостью числа обменов с внешней памятью для поиска любого ключа и тем, что это число обменов по причине сильной ветвистости деревьев не слишком велико при индексировании даже очень больших таблиц.
При использовании B+-деревьев для организации индексов каждая запись содержит упорядоченный список идентификаторов строк таблицы, включающих соответствующее значение ключа. Дополнительную сложность вызывает возможность организации индексов по нескольким столбцам таблицы (так называемых "составных" индексов). В этом случае в B+-дереве может появиться очень много избыточной информации по причине наличия в разных составных ключах общих подключей. Имеется ряд технических приемов сжатия индексов с составными ключами, улучшающих использование внешней памяти, но, естественно, замедляющих выполнение операций включения и исключения.
Разновидности полиморфизма
Полиморфизм в языках программирования - это очень широкое и собирательное понятие, включающее разные аспекты. Мы остановимся только на полиморфизме операций типов в контексте приведенного выше материала. Можно выделить две разновидности полиморфных операций: (1) одноименные операции одного или нескольких типов, различающиеся сигнатурами, и (2) операции с общей сигнатурой, определяемые и переопределяемые в иерархии наследования типов.
Как кажется, основной причиной появления полиморфизма первого типа является желание использовать для обозначения операций абстрактных типов привычные знаки операций, принятые во встроенных типах данных. Например, если определяется абстрактный тип данных "комплексные числа", то было бы естественно использовать знак "+" для обозначения сложения, "-" - для обозначения вычитания и т.д. Кроме того, для того же типа хотелось бы использовать один и тот же знак "+" для обозначения операций сложения двух комплексных чисел, сложения комплексного числа с вещественным и вещественного с комплексным.
Технику, обеспечивающую возможность ввести новую интерпретацию уже используемых знаков операций и/или имен функций и процедур, принято называть "перегрузкой". Перегрузка существует и в языках, не поддерживающих абстрактные типы данных, в частности, в языке программирования Ада. Но, с нашей точки зрения, особенно существенны возможности перегрузки именно в языках с абстрактными типами данных.
Преимуществом полиморфизма на основе перегрузки является то, что для его поддержки требуется не слишком существенное усложнение компилятора и не возникают дополнительные накладные расходы во время выполнения программы. Обычно реализация основывается на использовании сигнатур функций и процедур. При соблюдении обязательного требования различия сигнатур всех одноименных функций и процедур достаточно просто придумать правила формирования расширенных имен на основе основного имени функции или процедуры и имен типов ее параметров.
Если язык достаточно строго типизирован, и сигнатура любой доступной функции или процедуры находится в области видимости компилятора, то по имени и составу фактических параметров вызова можно определить расширенное имя требуемой подпрограммы. (Заметим, что если бы в программах на языке Си использование прототипов функций было бы обязательным, то можно было бы реализовать перегрузку имен функций и соответствующий полиморфизм даже в компиляторах чистого Си). Второй род полиморфизма операций типов и реализующих их функций и процедур возникает при переопределении в подтипе реализации операций супертипа. Как мы отмечали в предыдущем разделе, в этом случае сигнатуры операций изменяться не должны, и мы получаем разные реализации операции с одной сигнатурой. В этом случае возникающие неоднозначности невозможно разрешить во время компиляции программы, и приходится использовать упоминавшийся в предыдущем разделе метод позднего связывания. Тем самым, хотя отмеченные виды полиморфизма на первый взгляд кажутся очень близкими, они существенно по-разному реализуются и порождают существенно разные накладные расходы. При всей привлекательности возможности переопределения операций в подтипах ими следует пользоваться осмотрительно.
Реализация типа
Реализация типа представляет собой многовходовой программный модуль, точки входа которого соответствуют набору операций реализуемого типа. Естественно, должно иметься полное соответствие реализации типа его спецификации. Набор статических переменных (в смысле языков Си/Си++) этого модуля образует структуру данных, используемую для представления значений типа. Такой же структурой обладает любая переменная данного абстрактного типа.
Иногда для целей реализации типа бывает полезно иметь в составе его операций такие, которые недоступны для внешнего использования и носят служебный характер. Такие функции и/или процедуры специальным образом помечаются в реализации типа (например, как приватные), и их сигнатуры не включаются во внешнюю спецификацию типа. Переменные состояния, которые должны быть прямо доступны для внешнего использования, также помечаются специальным образом.
Сбалансированное многопутевое слияние
В основе метода внешней сортировки сбалансированным многопутевым слиянием является распределение серий исходного файла по m вспомогательным файлам B1, B2, ..., Bm и их слияние в m вспомогательных файлов C1, C2, ..., Cm. На следующем шаге производится слияние файлов C1, C2, ..., Cm в файлы B1, B2, ..., Bm и т.д., пока в B1 или C1 не образуется одна серия.
Многопутевое слияние является естественным развитием идеи обычного (двухпутевого) слияния, иллюстрируемого рисунком 2.14. Пример трехпутевого слияния показан на рисунке 3.3.
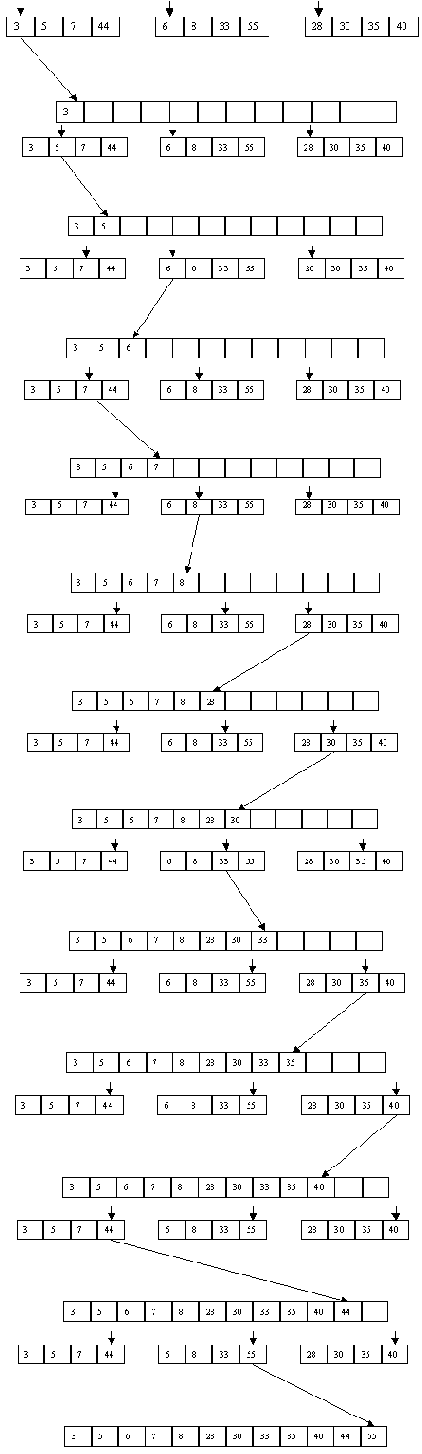
Рис. 3.3.
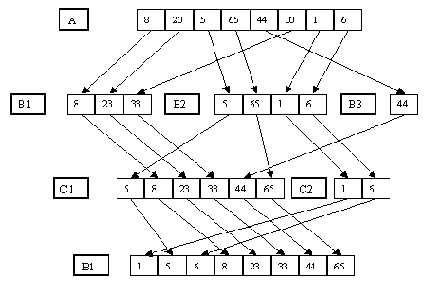
Рис. 3.4.
На рисунке 3.4 показан простой пример применения сортировки многопутевым слиянием. Он, конечно, слишком тривиален, чтобы продемонстрировать несколько шагов выполнения алгоритма, однако достаточен в качестве иллюстрации общей идеи метода. Заметим, что, как показывает этот пример, по мере увеличения длины серий вспомогательные файлы с большими номерами (начиная с номера n) перестают использоваться, поскольку им "не достается" ни одной серии. Преимуществом сортировки сбалансированным многопутевым слиянием является то, что число проходов алгоритма оценивается как O(log n) (n - число записей в исходном файле), где логарифм берется по основанию n. Порядок числа копирований записей - O(log n). Конечно, число сравнений не будет меньше, чем при применении метода простого слияния.
Сбалансированные двоичные деревья
Как видно из содержимого предыдущего подраздела, идеально сбалансированные деревья представляют, в большей степени, чисто теоретический интерес, поскольку поддержание идеальной сбалансированности требует слишком больших накладных расходов. В 1962 г. советские математики Адельсон-Вельский и Ландис предложили менее строгое определение сбалансированности деревьев, которое в достаточной степени обеспечивает возможности использования сбалансированных деревьев при существенно меньших расходах на поддержание сбалансированности. Такие деревья принято называть АВЛ-деревьями (в соответствии с именами их первооткрывателей).
По определению, двоичное дерево называется сбалансированным (или АВЛ) деревом в том и только в том случае, когда высоты двух поддеревьев каждой из вершин дерева отличаются не более, чем на единицу. При использовании деревьев, соответствующих этому определению, обеспечивается простая процедура балансировки при том, что средняя длина поиска составляет O(log n), т.е. практически не отличается от длины поиска в идеально сбалансированных деревьях. Как доказали Адельсон-Вельский и Ландис, АВЛ-дерево никогда не превышает по глубине аналогичное сбалансированное дерево больше, чем на 45%.
Чтобы понять, как устроены "самые плохие" АВЛ-деревья, попробуем построить сбалансированное дерево с высотой h, содержащее минимальное число вершин. Обозначим такое дерево через Th. Понятно, что T0 - это пустое дерево, а T1 - дерево с одной вершиной. Дерево Th строится путем добавления к корню двух поддеревьев типа T(h-1). Одно из таких поддеревьев должно иметь высоту h-1, а другое может иметь глубину h-2. Такие "плохо" сбалансированные деревья называются деревьями Фибоначчи (поскольку принцип их построения напоминает принцип построения чисел Фибоначчи) и определяются рекурсивно следующим образом: (a) пустое дерево есть дерево Фибоначчи высоты 0; (b) единственная вершина есть дерево Фибоначчи высоты 1; (c) если T(h-1) и T(h-2) являются деревьями Фибоначчи высотой h-1 и h-2 соответственно, а x - новый корень дерева, то Th = <T(h-1), x, T(h-2)> есть дерево Фибоначчи высотой h; (d) другие деревья Фибоначчи не существуют.
Примеры деревьев Фибоначчи высотой 2, 3 и 4 показаны на рисунке 4.11.

(а) Дерево Фибоначчи высотой 2

(b) Дерево Фибоначчи высотой 3

( c ) Дерево Фибоначчи высотой 4
Рис. 4.11. Примеры деревьев Фибоначчи Число вершин в дереве Th определяется из следующего рекуррентного соотношения: N0 = 0; N1 = 1; Nh = N(h-1) +1 + N(h-2) Эти числа определяют число вершин в АВЛ-дереве в худшем случае и называются "числами Леонарда". Заметим, что из этого соотношения следует, что длина пути от корня любого листа в АВЛ-дереве может отличаться не более, чем на единицу. Рассмотрим, как можно поддерживать балансировку АВЛ-дерева при выполнении операций включения и исключения ключей. Начнем с операции включения. Пусть рассматриваемое дерево состоит из корневой вершины r и левого (L) и правого (R) поддеревьев. Будем обозначать через hl высоту L, а через hr - высоту R. Для определенности будем считать, что новый ключ включается в поддерево L. Если высота L не изменяется, то не изменяются и соотношения между высотой L и R, и свойства АВЛ-дерева сохраняются. Если же при включении в поддерево L высота этого поддерева увеличивается на 1, то возможны следующие три случая: (a) если hl = hr, то после добавления вершины L и R станут разной высоты, но свойство сбалансированности сохранится; (b) если hl < hr, то после добавления новой вершины L и R станут равной высоты, т.е. сбалансированность общего дерева даже улучшится; (c) если hl > hr, то после включения ключа критерий сбалансированности нарушится, и потребуется перестройка дерева. Имеет смысл рассмотреть две разные ситуации. В первой ситуации новая вершина добавляется к левому поддереву L, во второй - к правому поддереву. Правила восстановления балансировки показаны на рисунке 4.12 и проиллюстрированы примерами на рисунке 4.13.

(a)

(b)

(c)

(d)
Рис. 4.12.

(a)

(b)

(c)

(d)
Рис. 4.13. Как кажется, в данном случае рисунки лучше проясняют суть явления, чем текст и тем более компьютерная программа. Действия, которые требуются для балансировки, авторы механизма назвали "поворотами".
Действительно, если внимательно посмотреть на то, что происходит с деревом, это действительно напоминает его повороты относительно выбранной вершины. При исключении вершин из АВЛ-дерева также возможна его не слишком сложная балансировка. Мы не будем приводить описание требующихся процедур, а проиллюстрируем их на нескольких последовательных примерах (рисунок 4.14).

(a)

(b)

(c)

(d)

(e)

(f)

(g)
Рис. 4.14. Известно, что оценкой стоимости поиска в АВЛ-дереве, а также выполнения операций включения и исключения ключей является O(log n), т.е. эти деревья при поиске ведут себя почти так же хорошо, как и идеально сбалансированные деревья, а поддержка балансировки при включениях и исключениях обходится гораздо дешевле.
Сортировка разделением (Quicksort)
Метод сортировки разделением был предложен Чарльзом Хоаром (он любит называть себя Тони) в 1962 г. Этот метод является развитием метода простого обмена и настолько эффективен, что его стали называть "методом быстрой сортировки - Quicksort".
Основная идея алгоритма состоит в том, что случайным образом выбирается некоторый элемент массива x, после чего массив просматривается слева, пока не встретится элемент a[i] такой, что a[i] > x, а затем массив просматривается справа, пока не встретится элемент a[j] такой, что a[j] < x. Эти два элемента меняются местами, и процесс просмотра, сравнения и обмена продолжается, пока мы не дойдем до элемента x. В результате массив окажется разбитым на две части - левую, в которой значения ключей будут меньше x, и правую со значениями ключей, большими x. Далее процесс рекурсивно продолжается для левой и правой частей массива до тех пор, пока каждая часть не будет содержать в точности один элемент. Понятно, что как обычно, рекурсию можно заменить итерациями, если запоминать соответствующие индексы массива. Проследим этот процесс на примере нашего стандартного массива (таблица 2.6).
Таблица 2.6. Пример быстрой сортировки
| Начальное состояние массива | 8 23 5 65 |44| 33 1 6 |
| Шаг 1 (в качестве x выбирается a[5]) | |--------| 8 23 5 6 44 33 1 65 |---| 8 23 5 6 1 33 44 65 |
| Шаг 2 (в подмассиве a[1], a[5] в качестве x выбирается a[3]) | 8 23 |5| 6 1 33 44 65 |--------| 1 23 5 6 8 33 44 65 |--| 1 5 23 6 8 33 44 65 |
| Шаг 3 (в подмассиве a[3], a[5] в качестве x выбирается a[4]) | 1 5 23 |6| 8 33 44 65 |----| 1 5 8 6 23 33 44 65 |
| Шаг 4 (в подмассиве a[3], a[4] выбирается a[4]) | 1 5 8 |6| 23 33 44 65 |--| 1 5 6 8 23 33 44 65 |
Алгоритм недаром называется быстрой сортировкой, поскольку для него оценкой числа сравнений и обменов является O(n?log n). На самом деле, в большинстве утилит, выполняющих сортировку массивов, используется именно этот алгоритм.
Сортировка с помощью дерева (Heapsort)
Начнем с простого метода сортировки с помощью дерева, при использовании которого явно строится двоичное дерево сравнения ключей. Построение дерева начинается с листьев, которые содержат все элементы массива. Из каждой соседней пары выбирается наименьший элемент, и эти элементы образуют следующий (ближе к корню уровень дерева). Из каждой соседней пары выбирается наименьший элемент и т.д., пока не будет построен корень, содержащий наименьший элемент массива. Двоичное дерево сравнения для массива, используемого в наших примерах, показано на рисунке 2.1. Итак, мы уже имеем наименьшее значение элементов массива. Для того, чтобы получить следующий по величине элемент, спустимся от корня по пути, ведущему к листу с наименьшим значением. В этой листовой вершине проставляется фиктивный ключ с "бесконечно большим" значением, а во все промежуточные узлы, занимавшиеся наименьшим элементом, заносится наименьшее значение из узлов - непосредственных потомков (рис. 2.2). Процесс продолжается до тех пор, пока все узлы дерева не будут заполнены фиктивными ключами (рисунки 2.3 - 2.8).
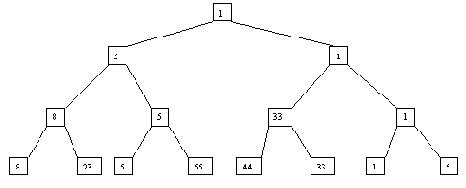
Рис. 2.1.
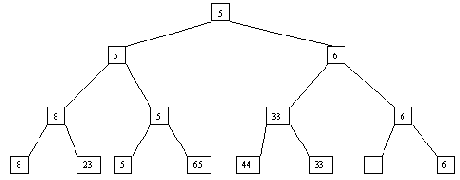
Рис. 2.2. Второй шаг
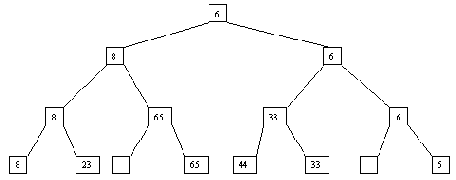
Рис. 2.3. Третий шаг
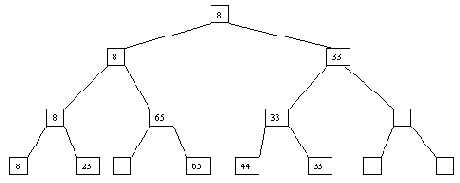
Рис. 2.4. четвертый шаг
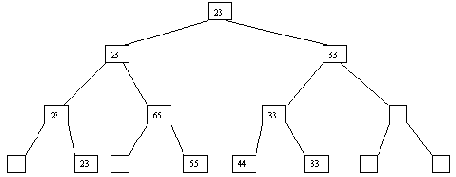
Рис. 2.5. Пятый шаг
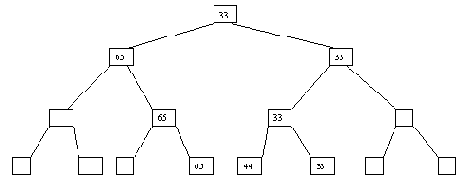
Рис. 2.6. Шестой шаг
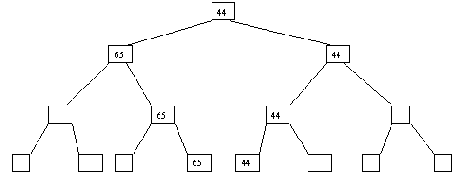
Рис. 2.7. Седьмой шаг
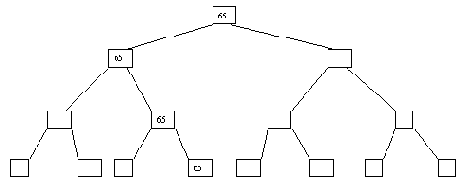
Рис. 2.8. Восьмой шаг
На каждом из n шагов, требуемых для сортировки массива, нужно log n (двоичный) сравнений. Следовательно, всего потребуется n?log n сравнений, но для представления дерева понадобится 2n - 1 дополнительных единиц памяти.
Имеется более совершенный алгоритм, который принято называть пирамидальной сортировкой (Heapsort). Его идея состоит в том, что вместо полного дерева сравнения исходный массив a[1], a[2], ..., a[n] преобразуется в пирамиду, обладающую тем свойством, что для каждого a[i] выполняются условия a[i] <= a[2i] и a[i] <= a[2i+1]. Затем пирамида используется для сортировки.
Наиболее наглядно метод построения пирамиды выглядит при древовидном представлении массива, показанном на рисунке 2.9. Массив представляется в виде двоичного дерева, корень которого соответствует элементу массива a[1].
На втором ярусе находятся элементы a[2] и a[3]. На третьем - a[4], a[5], a[6], a[7] и т.д. Как видно, для массива с нечетным количеством элементов соответствующее дерево будет сбалансированным, а для массива с четным количеством элементов n элемент a[n] будет единственным (самым левым) листом "почти" сбалансированного дерева.
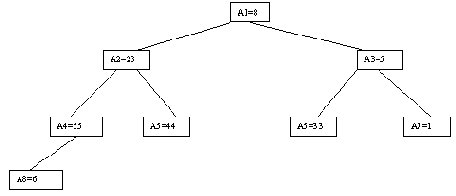
Рис. 2.9. Очевидно, что при построении пирамиды нас будут интересовать элементы a[n/2], a[n/2-1], ..., a[1] для массивов с четным числом элементов и элементы a[(n-1)/2], a[(n-1)/2-1], ..., a[1] для массивов с нечетным числом элементов (поскольку только для таких элементов существенны ограничения пирамиды). Пусть i - наибольший индекс из числа индексов элементов, для которых существенны ограничения пирамиды. Тогда берется элемент a[i] в построенном дереве и для него выполняется процедура просеивания, состоящая в том, что выбирается ветвь дерева, соответствующая min(a[2?i], a[2?i+1]), и значение a[i] меняется местами со значением соответствующего элемента. Если этот элемент не является листом дерева, для него выполняется аналогичная процедура и т.д. Такие действия выполняются последовательно для a[i], a[i-1], ..., a[1]. Легко видеть, что в результате мы получим древовидное представление пирамиды для исходного массива (последовательность шагов для используемого в наших примерах массива показана на рисунках 2.10-2.13).
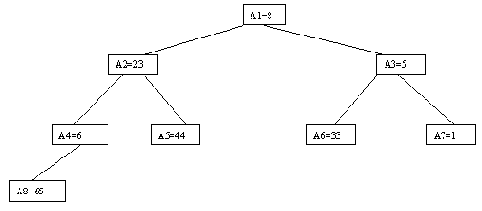
Рис. 2.10.
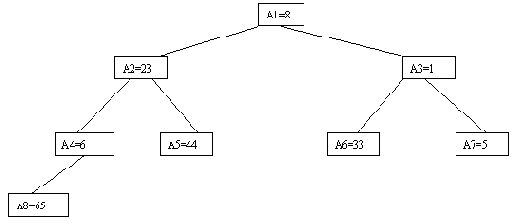
Рис. 2.11.
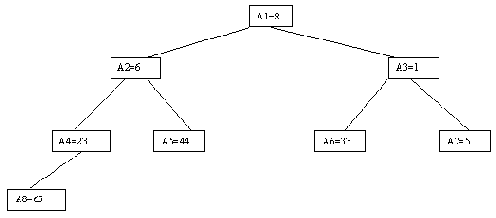
Рис. 2.12.
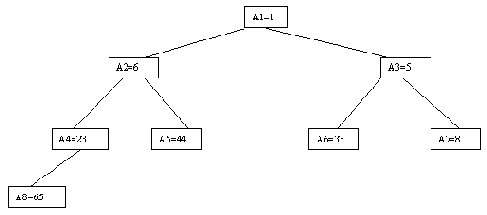
Рис. 2.13. В 1964 г. Флойд предложил метод построения пирамиды без явного построения дерева (хотя метод основан на тех же идеях). Построение пирамиды методом Флойда для нашего стандартного массива показано в таблице 2.7. Таблица 2.7 Пример построения пирамиды
| Начальное состояние массива | 8 23 5 |65| 44 33 1 6 |
| Шаг 1 | 8 23 |5| 6 44 33 1 65 |
| Шаг 2 | 8 |23| 1 6 44 33 5 65 |
| Шаг 3 | |8| 6 1 23 44 33 5 65 |
| Шаг 4 | 1 6 8 23 44 33 5 65 1 6 5 23 44 33 8 65 |
Пусть i - наибольший индекс массива, для которого существенны условия пирамиды. Тогда начиная с a[1] до a[i] выполняются следующие действия. На каждом шаге выбирается последний элемент пирамиды (в нашем случае первым будет выбран элемент a[8]). Его значение меняется со значением a[1], после чего для a[1] выполняется просеивание. При этом на каждом шаге число элементов в пирамиде уменьшается на 1 (после первого шага в качестве элементов пирамиды рассматриваются a[1], a[2], ..., a[n-1]; после второго - a[1], a[2], ..., a[n-2] и т.д., пока в пирамиде не останется один элемент). Легко видеть (это иллюстрируется в таблице 2.8), что в результате мы получим массив, упорядоченный в порядке убывания. Можно модифицировать метод построения пирамиды и сортировки, чтобы получить упорядочение в порядке возрастания, если изменить условие пирамиды на a[i] >= a[2?i] и a[1] >= a[2?i+1] для всех осмысленных значений индекса i. Таблица 2.8 Сортировка с помощью пирамиды
| Исходная пирамида | 1 6 5 23 44 33 8 65 |
| Шаг 1 | 65 6 5 23 44 33 8 1 5 6 65 23 44 33 8 1 5 6 8 23 44 33 65 1 |
| Шаг 2 | 65 6 8 23 44 33 5 1 6 65 8 23 44 33 5 1 6 23 8 65 44 33 5 1 |
| Шаг 3 | 33 23 8 65 44 6 5 1 8 23 33 65 44 6 5 1 |
| Шаг 4 | 44 23 33 65 8 6 5 1 23 44 33 65 8 6 5 1 |
| Шаг 5 | 65 44 33 23 8 6 5 1 33 44 65 23 8 6 5 1 |
| Шаг 6 | 65 44 33 23 8 6 5 1 44 65 33 23 8 6 5 1 |
| Шаг 7 | 65 44 33 23 8 6 5 1 |
Сортировка со слиянием
Сортировки со слиянием, как правило, применяются в тех случаях, когда требуется отсортировать последовательный файл, не помещающийся целиком в основной памяти. Методам внешней сортировки посвящается следующая часть книги, в которой основное внимание будет уделяться методам минимизации числа обменов с внешней памятью. Однако существуют и эффективные методы внутренней сортировки, основанные на разбиениях и слияниях.
Один из популярных алгоритмов внутренней сортировки со слияниями основан на следующих идеях (для простоты будем считать, что число элементов в массиве, как и в нашем примере, является степенью числа 2). Сначала поясним, что такое слияние. Пусть имеются два отсортированных в порядке возрастания массива p[1], p[2], ..., p[n] и q[1], q[2], ..., q[n] и имеется пустой массив r[1], r[2], ..., r[2?n], который мы хотим заполнить значениями массивов p и q в порядке возрастания. Для слияния выполняются следующие действия: сравниваются p[1] и q[1], и меньшее из значений записывается в r[1]. Предположим, что это значение p[1]. Тогда p[2] сравнивается с q[1] и меньшее из значений заносится в r[2]. Предположим, что это значение q[1]. Тогда на следующем шаге сравниваются значения p[2] и q[2] и т.д., пока мы не достигнем границ одного из массивов. Тогда остаток другого массива просто дописывается в "хвост" массива r.
Пример слияния двух массивов показан на рисунке 2.14.
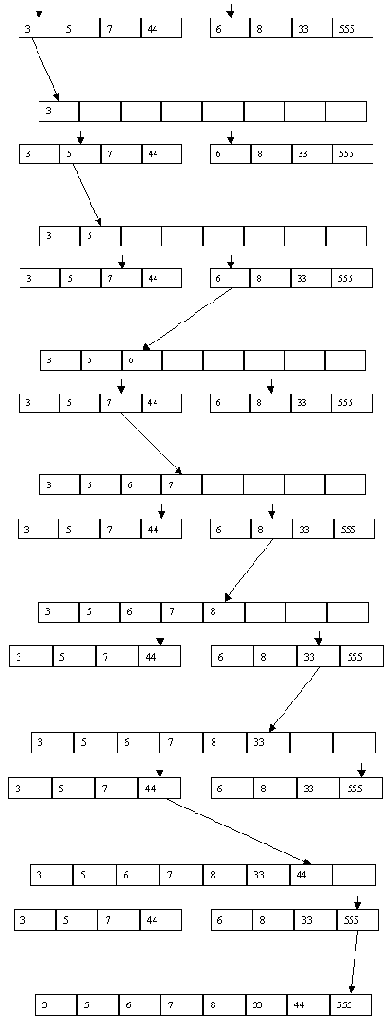
Рис. 2.14.
Для сортировки со слиянием массива a[1], a[2], ..., a[n] заводится парный массив b[1], b[2], ..., b[n]. На первом шаге производится слияние a[1] и a[n] с размещением результата в b[1], b[2], слияние a[2] и a[n-1] с размещением результата в b[3], b[4], ..., слияние a[n/2] и a[n/2+1] с помещением результата в b[n-1], b[n]. На втором шаге производится слияние пар b[1], b[2] и b[n-1], b[n] с помещением результата в a[1], a[2], a[3], a[4], слияние пар b[3], b[4] и b[n-3], b[n-2] с помещением результата в a[5], a[6], a[7], a[8], ..., слияние пар b[n/2-1], b[n/2] и b[n/2+1], b[n/2+2] с помещением результата в a[n-3], a[n-2], a[n-1], a[n].
И т.д. На последнем шаге, например (в зависимости от значения n), производится слияние последовательностей элементов массива длиной n/2 a[1], a[2], ..., a[n/2] и a[n/2+1], a[n/2+2], ..., a[n] с помещением результата в b[1], b[2], ..., b[n]. Для случая массива, используемого в наших примерах, последовательность шагов показана в таблице 2.9.
Таблица 2.9. Пример сортировки со слиянием
| Начальное состояние массива | 8 23 5 65 44 33 1 6 |
| Шаг 1 | 6 8 1 23 5 33 44 65 |
| Шаг 2 | 6 8 44 65 1 5 23 33 |
| Шаг 3 | 1 5 6 8 23 33 44 65 |
Сортировка включением
Одним из наиболее простых и естественных методов внутренней сортировки является сортировка с простыми включениями. Идея алгоритма очень проста. Пусть имеется массив ключей a[1], a[2], ..., a[n]. Для каждого элемента массива, начиная со второго, производится сравнение с элементами с меньшим индексом (элемент a[i] последовательно сравнивается с элементами a[i-1], a[i-2] ...) и до тех пор, пока для очередного элемента a[j] выполняется соотношение a[j] > a[i], a[i] и a[j] меняются местами. Если удается встретить такой элемент a[j], что a[j] <= a[i], или если достигнута нижняя граница массива, производится переход к обработке элемента a[i+1] (пока не будет достигнута верхняя граница массива).
Легко видеть, что в лучшем случае (когда массив уже упорядочен) для выполнения алгоритма с массивом из n элементов потребуется n-1 сравнение и 0 пересылок. В худшем случае (когда массив упорядочен в обратном порядке) потребуется n?(n-1)/2 сравнений и столько же пересылок. Таким образом, можно оценивать сложность метода простых включений как O(n2).
Можно сократить число сравнений, применяемых в методе простых включений, если воспользоваться тем фактом, что при обработке элемента a[i] массива элементы a[1], a[2], ..., a[i-1] уже упорядочены, и воспользоваться для поиска элемента, с которым должна быть произведена перестановка, методом двоичного деления. В этом случае оценка числа требуемых сравнений становится O(n?log n). Заметим, что поскольку при выполнении перестановки требуется сдвижка на один элемент нескольких элементов, то оценка числа пересылок остается O(n2).
| Начальное состояние массива | 8 23 5 65 44 33 1 6 |
| Шаг 1 | 8 23 5 65 44 33 1 6 |
| Шаг 2 | 8 5 23 65 44 33 1 6 5 8 23 65 44 33 1 6 |
| Шаг 3 | 5 8 23 65 44 33 1 6 |
| Шаг 4 | 5 8 23 44 65 33 1 6 |
| Шаг 5 | 5 8 23 44 33 65 1 6 5 8 23 33 44 65 1 6 |
| Шаг 6 | 5 8 23 33 44 1 65 6 5 8 23 33 1 44 65 6 5 8 23 1 33 44 65 6 5 8 1 23 33 44 65 6 5 1 8 23 33 44 65 6 1 5 8 23 33 44 65 6 |
| Шаг 7 | 1 5 8 23 33 44 6 65 1 5 8 23 33 6 44 65 1 5 8 23 6 33 44 65 1 5 8 6 23 33 44 65 1 5 6 8 23 33 44 65 |
Дальнейшим развитием метода сортировки с включениями является сортировка методом Шелла, называемая по-другому сортировкой включениями с уменьшающимся расстоянием.
Мы не будем описывать алгоритм в общем виде, а ограничимся случаем, когда число элементов в сортируемом массиве является степенью числа 2. Для массива с 2n элементами алгоритм работает следующим образом. На первой фазе производится сортировка включением всех пар элементов массива, расстояние между которыми есть 2(n-1). На второй фазе производится сортировка включением элементов полученного массива, расстояние между которыми есть 2(n-2). И так далее, пока мы не дойдем до фазы с расстоянием между элементами, равным единице, и не выполним завершающую сортировку с включениями. Применение метода Шелла к массиву, используемому в наших примерах, показано в таблице 2.2.
Таблица 2.2. Пример сортировки методом Шелл
| Начальное состояние массива | 8 23 5 65 44 33 1 6 |
| Фаза 1 (сортируются элементы, расстояние между которыми четыре) | 8 23 5 65 44 33 1 6 8 23 5 65 44 33 1 6 8 23 1 65 44 33 5 6 8 23 1 6 44 33 5 65 |
| Фаза 2 (сортируются элементы, расстояние между которыми два) | 1 23 8 6 44 33 5 65 1 23 8 6 44 33 5 65 1 23 8 6 5 33 44 65 1 23 5 6 8 33 44 65 1 6 5 23 8 33 44 65 1 6 5 23 8 33 44 65 1 6 5 23 8 33 44 65 |
| Фаза 3 (сортируются элементы, расстояние между которыми один) | 1 6 5 23 8 33 44 65 1 5 6 23 8 33 44 65 1 5 6 23 8 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 1 5 6 8 23 33 44 65 |
Сортировка выбором
При сортировке массива a[1], a[2], ..., a[n] методом простого выбора среди всех элементов находится элемент с наименьшим значением a[i], и a[1] и a[i] обмениваются значениями. Затем этот процесс повторяется для получаемых подмассивов a[2], a[3], ..., a[n], ... a[j], a[j+1], ..., a[n] до тех пор, пока мы не дойдем до подмассива a[n], содержащего к этому моменту наибольшее значение. Работа алгоритма иллюстрируется примером в таблице 2.5.
Таблица 2.5. Пример сортировки простым выбором
| Начальное состояние массива | 8 23 5 65 44 33 1 6 |
| Шаг 1 | 1 23 5 65 44 33 8 6 |
| Шаг 2 | 1 5 23 65 44 33 8 6 |
| Шаг 3 | 1 5 6 65 44 33 8 23 |
| Шаг 4 | 1 5 6 8 44 33 65 23 |
| Шаг 5 | 1 5 6 8 33 44 65 23 |
| Шаг 6 | 1 5 6 8 23 44 65 33 |
| Шаг 7 | 1 5 6 8 23 33 65 44 |
| Шаг 8 | 1 5 6 8 23 33 44 65 |
Для метода сортировки простым выбором требуемое число сравнений - nx(n-1)/2. Порядок требуемого числа пересылок (включая те, которые требуются для выбора минимального элемента) в худшем случае составляет O(n2). Однако порядок среднего числа пересылок есть O(n?ln n), что в ряде случаев делает этот метод предпочтительным.
Совершенное хэширование
Вырожденный пример абсолютно совершенной хэш-функции приведен на рисунке 4.17, где ключами являются коды заглавных букв латинского алфавита (в кодировке ASCII), а хэш-функция отрезает от кода буквы младшие пять бит.

Рис. 4.17.
В более сложных случаях для построения совершенной хэш-функции используются специальные программы (основанные на эмпирических алгоритмах), которые по заданному набору ключей генерируют функции отображения ключей в индексы массивов хранимых записей. Вообще говоря, выработанная совершенная хэш-функция не гарантирует, что все элементы массива будут заполнены записями, соответствующими значениям ключей. Более того, при добавлении хотя бы одного нового ключа к ранее заданному набору потребуется генерация новой хэш-функции и соответствующая ей перестановка элементов массива записей.
Прием совершенного хэширования дает превосходные результаты при задании известного заранее не очень большого набора ключей, но не помогает в случае необходимости динамического включения или исключения записей.
Сравнение методов внутренней сортировки
Для рассмотренных в начале этой части простых методов сортировки существуют точные формулы, вычисление которых дает минимальное, максимальное и среднее число сравнений ключей (C) и пересылок элементов массива (M). Таблица 2.10 содержит данные, приводимые в книге Никласа Вирта.
Таблица 2.10. Характеристики простых методов сортировки
| Min | Avg | Max | |
| Прямое включение |
C = n-1 M = 2x(n-1) |
(n2 + n - 2)/4 (n2 - 9n - 10)/4 |
(n2 -n)/2 - 1 (n2 -3n - 4)/2 |
| Прямой выбор |
C = (n2 - n)/2 M = 3x(n-1) |
(n2 - n)/2 nx(ln n + 0.57) |
(n2 - n)/2 n2/4 + 3x(n-1) |
| Прямой обмен |
C = (n2 - n)/2 M = 0 |
(n2 - n)/2 (n2 - n)x0.75 |
(n2 - n)/2 (n2 - n)x1.5 |
Для оценок сложности усовершенствованных методов сортировки точных формул нет. Известно лишь, что для сортировки методом Шелла порядок C и M есть O(n(1.2)), а для методов Quicksort, Heapsort и сортировки со слиянием - O(n?log n). Однако результаты экспериментов показывают, что Quicksort показывает результаты в 2-3 раза лучшие, чем Heapsort (в таблице 2.11 приводится выборка результатов из таблицы, опубликованной в книге Вирта; результаты получены при прогоне программ, написанных на языке Модула-2). Видимо, по этой причине именно Quicksort обычно используется в стандартных утилитах сортировки (в частности, в утилите sort, поставляемой с операционной системой UNIX).
Таблица 2.11. Время работы программ сортировки
| Упорядоченный массив | Случайный массив | В обратном порядке | |
| n = 256 | |||
|
Heapsort Quicksort Сортировка со слиянием |
0.20 0.20 0.20 |
0.08 0.12 0.08 |
0.18 0.18 0.18 |
| n = 2048 | |||
|
Heapsort Quicksort Сортировка со слиянием |
2.32 2.22 2.12 |
0.72 1.22 0.76 |
1.98 2.06 1.98 |
Строчные типы данных
Одним из недостатков классического реляционного подхода к построению баз данных является то, что при определении схемы таблицы ее имя одновременно становится именем самой таблицы. Т.е. отсутствует возможность отдельно определить именованную схему таблицы, а затем - одну или несколько таблиц с той же самой схемой. Для устранения этого недостатка (а также получения некоторых дополнительных преимуществ; см. ниже) в объектно-реляционных системах появилось понятие строчного типа.
Фактически, строчный тип - это именованная спецификация одного или более столбцов (для каждого столбца указывается имя, а также его тип или домен). После определения строчного типа можно специфицировать таблицы, заголовок которых соответствует этому типу или включает его как свою часть.
Типы и структуры данных
Типы и структуры данных представляют собой фундамент, на котором строится вся современная технология программирования. Программирования в широком смысле, включая не только непосредственно написание и отладку программ, но и проектирование программных систем разной сложности; проектирование, реализацию и использование баз данных и информационных систем и т.д. Сегодня только большие любители обходятся без использования безтиповых языков программирования (например, языков ассемблера) или неструктурированных и/или нетипизированных хранилищ данных во внешней памяти. В этой части книги, не прибегая к излишним формализмам и теоретическим изыскам, мы приводим систематическое обсуждение основных типов и структур данных, применяемых в современных языках программирования, а также соответствующих концепций, используемых в распространенных реляционных и перспективных объектно-реляционных системах.
Типы и структуры данных, применяемые в реляционных базах данных
В конце этой части книги мы коротко рассмотрим особенности использования типов и структур данных в системах управления базами данных (СУБД). Начнем с наиболее распространенных сегодня традиционных баз данных, основанных на чистой, классической реляционной модели данных. Одним из базовых свойств этой модели является атомарность значений в каждом из столбцов таблиц, составляющих базу данных. Другими словами, эти значения должны принадлежать к одному из встроенных типов, поддерживаемых СУБД.
Практически все современные реляционные СУБД опираются на стандартный язык баз данных SQL и поддерживают встроенные типы данных, специфицированные в этом языке. Если не вдаваться в синтаксические детали, то типы данных в стандарте языка SQL/92 определяются следующим образом:
Тип данных определяется как множество представляющих его значений. Логическим представлением значения является литерал. Физическое представление зависит от реализации.
Значение любого типа является примитивным в том смысле, что в соответствии со стандартом оно не может быть логически разбито на другие значения. Значения могут быть определенными или неопределенными. Неопределенное значение - это зависящее от реализации значение, которое гарантированно отлично от любого определенного значения соответствующего типа. Можно считать, что имеется всего одно неопределенное значение, входящее в любой тип данных языка SQL. Для неопределенного значения отсутствует представляющий его литерал, хотя в некоторых случаях используется ключевое слово NULL для выражения того, что желательно именно неопределенное значение.
SQL/92 определяются типы данных, обозначаемые следующими ключевыми словами: CHARACTER, CHARACTER VARYING, BIT, BIT VARYING, NUMERIC, DECIMAL, INTEGER, SMALLINT, FLOAT, REAL, DOUBLE PRECISION, DATE, TIME, TIMESTAMP и INTERVAL.
Типы данных CHARACTER и CHARACTER VARYING совместно называются типами данных символьных строк; типы данных BIT и BIT VARYING - типами данных битовых строк. Типы данных символьных строк и типы данных битовых строк совместно называются строчными типами данных, а значения строчных типов называются строками.
Типы данных NUMERIC, DECIMAL, INTEGER и SMALLINT совместно называются типами данных точных чисел.
Типы данных FLOAT, REAL и DOUBLE PRECISION совместно называются типами данных приблизительных чисел. Типы данных точных чисел и типы данных приблизительных чисел совместно называются числовыми типами. Значения числовых типов называются числами. Типы данных DATE, TIME и TIMESTAMP совместно называются типами даты-времени. Значения типов даты-времени называются "дата-время". Тип данных INTERVAL называется интервальным типом. Поскольку основным способом использования языка SQL при создании прикладных информационных систем является встраивание операторов SQL в программы, написанные на традиционных языках программирования, необходимо для всех потенциально используемых языков программирования иметь правила соответствия встроенных типов SQL встроенным типам соответствующих языков. Стандарт обеспечивает такие соответствия. В частности, для языка Си установлены следующие соответствия: CHARACTER соответствует строкам Си (массивам символов, завершающимся "пустым" символом); INTEGER соответствует long; SMALLINT соответствует short; REAL соответствует float; DOUBLE PRECISION соответствует double. Естественно, это не означает, что в базах данных числа хранятся именно в той форме, в которой они представляются в Си-программе. Необходимые преобразования представлений обеспечиваются на интерфейсе прикладной программы и СУБД. Важным понятием реляционных баз данных, зафиксированным в стандарте языка SQL, является понятие домена. Домен - это именованное множество значений некоторого встроенного типа, ограниченное условием, задаваемым при определении домена. Условие определяет вхождение значения базового типа во множество значений домена. В некотором смысле можно считать понятие домена расширением понятия ограниченного типа в языках программирования. В частности, если столбец C некоторой таблицы определен на домене D, то система гарантирует, что в этом столбце будут присутствовать только значения домена D. Кроме того, считается допустимым соединять таблицы T1 и T2 по значениям столбцов C1 и C2 только в том случае, когда C1 и C2 определены на общем домене D. Значения всех упомянутых типов (и определенных на них доменов) имеют фиксированную или, по крайней мере, ограниченную длину.Даже для типов CHARACTER VARYING и BIT VARYING длина допустимого значения обычно ограничена размером страниц внешней памяти, используемых СУБД для хранения баз данных. В связи с потребностями современных приложений (географических, мультимедийных, категории CAD/CAM и т.д.) в большинстве СУБД поддерживается дополнительный, не специфицированный в стандарте SQL псевдотип данных с собирательным названием BLOB (Binary Large Object). Значения этого типа представляют собой последовательности байт, на которые на уровне СУБД не накладывается никакая более сложная структура и длина которых практически не ограничена (в 32-разрядных архитектурах - до 2 Гбт). Необходимая структуризация значений типа BLOB производится на прикладном уровне. Традиционные СУБД обеспечивают очень примитивный набор операций со столбцами типа BLOB - выбрать значение столбца в основную память или в файл и занести в столбец значение из основной памяти или файла.
Типы и структуры данных, применяемые в объектно-реляционных базах данных
Чисто реляционные базы данных обладают рядом ограничений, которые затрудняют их использование в приложениях, требующих богатого типового окружения. Это относится и к категорическому требованию использовать в столбцах таблиц только атомарные значения встроенных типов, и к невозможности определить новые типы данных (возможно, с атомарными значениями) с дополнительными или переопределенными операциями. Понятно, что ослабление этих ограничений приводит к потребности существенного пересмотра архитектуры серверных продуктов баз данных. В этой книге не рассматриваются требуемые архитектурные расширения и переделки. Мы остановимся только на расширениях системы типов и связанных с этим структурах данных.
В настоящее время отсутствует общая точка зрения относительно того, что должна обеспечивать объектно-реляционная СУБД по части обеспечения типовой среды (похоже, что до принятия следующего стандарта - SQL-3 - окончательной ясности так и не будет). Однако наличие на рынке по крайней мере трех развитых систем с объектно-реляционными расширениями дает возможность сделать небольшой предварительный обзор обязательных возможностей.
Типы коллекций
Типы коллекций находятся ближе всего к конструируемым типам языков программирования и внедряются в объектно-реляционные базы данных, чтобы ликвидировать или, по крайней мере, смягчить ограничение первой нормальной формы (атомарности значений столбцов), накладываемое классической реляционной моделью данных. К типам коллекций относятся типы массива, списка и множества. Заметим, что в данном случае (в отличие от языков программирования) не устанавливаются ограничения на мощность базового типа множества (в силу специфики расположения данных во внешней памяти).
Для каждой разновидности типа коллекции имеется предопределенный набор операций (например, доступ к элементу массива по индексу). После определения любого типа коллекции его можно использовать как любой встроенный тип. В частности, типом столбца таблицы может быть тип множества, базовым типом которого является строчный тип. Понятно, что с использованием типов коллекций можно организовывать базы данных с произвольно сложной иерархической структурой.
Указатели
Понятие указателя в языках программирования является абстракцией понятия машинного адреса. Подобно тому, как зная машинный адрес можно обратиться к нужному элементу памяти, имея значение указателя, можно обратиться к соответствующей переменной. Различие между механизмами указателей в разных языках состоит главным образом в том, откуда берется значение указателя. Чем больше возможностей по работе с указателями, тем более эффективную программу можно написать и тем "опаснее" становится программирование. Обычно возможности оперирования указателями ограничиваются по мере повышения уровня языка и усиления его типизации.
В любом случае для объявления указательных переменных служат так называемые указательные, или ссылочные типы. Для определения указательного типа, значениями которого являются указатели на переменные встроенного или ранее определенного типа T0, в языке Паскаль используется конструкция type T = T0. В языке Си отсутствуют отдельные возможности определения указательного типа, и, чтобы объявить переменную var, которая будет содержать указатели на переменные типа T0, используется конструкция T0 *var. Но конечно, это чисто поверхностное отличие, а суть гораздо глубже.
В языках линии Паскаль переменной указательного типа можно присваивать только значения, вырабатываемые встроенной процедурой динамического выделения памяти new, значения переменных того же самого указательного типа и специальное "пустое" ссылочное значение nil, которое входит в любой указательный тип. Не допускаются преобразования типов указателей и какие-либо арифметические действия над их значениями. С переменной-указателем var можно выполнять только операцию var, обеспечивающую доступ к значению переменной типа T0, на которую указывает значение переменной var.
Напротив, в языках Си и Си++ имеется полная свобода работы с указателями. С помощью операции "&" можно получить значение указателя для любой переменной, над указателями определены арифметические действия, возможно явное преобразование указательных типов и даже преобразование целых типов к указательным типам.
В этих языках не фиксируется значение "пустых" (ни на что не ссылающихся) указательных переменных. Имеется лишь рекомендация использовать в качестве такого значения константу с символическим именем NULL, определяемую в библиотечном файле включения. По сути дела, понятие указателя в этих языках очень близко к понятию машинного адреса. Отмеченные свойства механизма указателей существенно повлияли на особенности реализации в языках Си и Си++ работы с массивами. Имя массива в этих языках интерпретируется как имя константного указателя на первый элемент массива. Операция доступа к i-тому элементу массива arr хотя и обозначается как и в языках линии Паскаль arr[i], имеет низкоуровневую интерпретацию *(arr+i). Поэтому было логично допустить подобную запись для любой переменной var с указательным типом: var[i] интерпретируется как *(var+i). По этой причине понятие массива в Си/Си++ существенно отличается от соответствующего понятия в Паскале. Размер массива существенен только при его определении и используется для выделения соответствующего объема памяти. При работе программы используется только имя массива как константный указатель соответствующего типа. Нет операций над "массивными переменными" целиком; в частности, невозможно присваивание. Фактически отсутствует поддержка массивов как параметров вызова функций - передаются именно значения указателей (в связи с этим, при описании формального параметра-массива его размер не указывается). Функции не могут вырабатывать "массивные" значения. Как отмечалось выше, особенности работы с указателями в некоторой степени повлияли и на организацию структур. Хотя в описаниях языков Си и Си++ и рекомендациях по программированию присутствует настоятельный совет обращаться к полям структурных переменныхтолько по их именам, известно, что каждое имя на самом деле интерпретируется как смещение от начала структуры. Поэтому, имея значение указателя на начало структурной переменной и манипулируя известными длинами полей структуры, технически можно добраться до любого поля, не используя его имя. Подводя итоги этого краткого обсуждения механизма указателей в Си/Си++, заметим, что позволяя программировать с очень большой эффективностью, этот механизм делает языки очень опасными для использования и требует от программистов большой аккуратности и сдержанности.При разработке получающего все большее распространение языка Java (одним из основных предков которого был Си++) для повышения уровня безопасности были резко ограничены именно средства работы с указателями в языке Си++.
Улучшение эффективности внешней сортировки за счет использования основной памяти
Понятно, что чем более длинные серии содержит файл перед началом применения внешней сортировки, тем меньше потребуется слияний и тем быстрее закончится сортировка. Поэтому до начала применения любого из методов внешней сортировки, основанных на применении серий, начальный файл частями считывается в основную память, к каждой части применяется один из наиболее эффективных алгоритмов внутренней сортировки (обычно Quicksort или Heapsort) и отсортированные части (образующие серии) записываются в новый файл (в старый нельзя, потому что он чисто последовательный).
Кроме того, конечно, при выполнении распределений и слияний используется буферизация блоков файла(ов) в основной памяти. Возможный выигрыш в производительности зависит от наличия достаточного числа буферов достаточного размера.
Уточняемые типы данных
Никлас Вирт называет такие типы ограниченными (restricted). На самом деле, ни этот термин, ни тот, который употребляем мы в этой книге, не являются абсолютно правильно отражающими суть соответствующего механизма. Все же, по нашему мнению, термин "уточняемый тип" немного ближе по смыслу.
Суть состоит в том, что для любого значения любого встроенного (и перечисляемого) типа существует его внешнее литеральное представление. Более того, по литеральному представлению константы можно однозначно определить тип, к которому она относится. Если к тому же на множестве значений типа задано отношение порядка (определены операции сравнения), то иногда возникает потребность сказать, что в данном приложении нас интересует подмножество значений такого типа, ограниченное некоторым специфицированным диапазоном. По причине наличия упорядоченности значений такой диапазон может быть задан парой литеральных констант базового типа c1 и c2, удовлетворяющих условию c1 <= c2. Тем самым, определение нового уточненного типа может иметь вид (пример из языка Модула-2): TYPE T = [c1..c2].
Почему мы предпочитаем использовать термин "уточняемый тип"? Основная причина состоит в том, что "ограниченные типы" в том смысле, в котором они используются в языках линии Паскаль, являются частным случаем более общего понятия, используемого в языках баз данных и именуемого "доменом". При определении домена тоже накладывается некоторое ограничение на значения базового типа, но это ограничение может выражаться в виде произвольного логического выражения, а не только с помощью указания диапазона. То есть мы действительно уточняем характеристики базового типа.
Основной проблемой уточняемых типов является потребность в динамическом контроле значений, формируемых при вычислении выражений и возвращаемых функциями. Если для значений базовых типов (по крайней мере, числовых) такой контроль, как правило, поддерживается аппаратурой компьютера, то для уточняемых типов, вообще говоря, требуется программный контроль, вызывающий серьезные накладные расходы. В развитых компиляторах обычно поддерживаются два режима компиляции - отладочный со всеми возможными контролирующими действиями во время выполнения программы и "боевой", в котором контроль отключается. Однако, если учесть, что в любой серьезной программе ошибки сохраняются на протяжении всей ее жизни, бесконтрольное выполнение программ очень затрудняет нахождение таких ошибок.
Встроенные типы данных
Обычно в состав встроенных типов данных включаются такие типы, операции над значениями которых напрямую или, по крайней мере, достаточно эффективно поддерживаются командами компьютеров. В современных компьютерах к таким "машинным" типам относятся целые числа разного размера (от одного до восьми байт), булевские значения (поддерживаемые обычно за счет наличия признаков условной передачи управления) и числа с плавающей точкой одинарной и двойной точности (обычно четыре и восемь байт соответственно). В более ранних компьютерах часто поддерживалась десятичная арифметика с фиксированной точкой (например, в мейнфреймах компании IBM и супер-миникомпьютерах компании Digital), но в настоящее время прямая аппаратная поддержка такой арифметики отсутствует практически во всех распространенных процессорах.
В соответствии с этим, в традиционный набор встроенных типов обычно входят следующие (мы будем говорить про размеры внутреннего представления значений этих типов, хотя в спецификациях языков такая информация, как правило, отсутствует):
Тип CHARACTER (или CHAR) в разных языках - это либо набор печатных символов из алфавита, зафиксированного в описании языка (для большинства языков англоязычного происхождения этот алфавит соответствует кодовому набору ASCII); либо произвольная комбинация нулей и единиц, размещаемых в одном байте.
В первой интерпретации (свойственной языкам линии Паскаль) для значений типа CHAR определены только операции сравнения в соответствии с принятым алфавитом. Например, при использовании ASCII выполняются соотношения 0 < 1 < ...< 9 < A < B < ...< Z < a < b < ...< z; известно, что если значение переменной x удовлетворяет условию 0 <= x <= 9, то это значение - цифра; если A <= x <= Z, то значение x - прописная буква; если a <= x <= z, то значение x - строчная буква и т.д. При использовании этой интерпретации арифметические операции над символьными значениями не допускаются.
Во второй интерпретации (свойственной языкам линии Си) литеральными константами типа CHAR по-прежнему могут быть печатные символы из принятого в языке алфавита, но возможно использование и числовых констант, задающих желаемое содержимое байта.
В этом случае, как правило, над значениями типа CHAR возможно выполнение не только операций сравнения, но и операций целочисленной арифметики. Наконец, в некоторых языках явно различают тип CHAR как чисто символьный тип и тип сверхмалых целых (TINY INTEGER) как тип целых чисел со значениями, умещающимися в один байт. В современных компьютерах, как правило, поддерживается целочисленная байтовая арифметика, обеспечивающая как первую, так и вторую интерпретацию типа CHAR. Тип BOOLEAN в тех языках, где он явно поддерживается, содержит два значения - TRUE (истина) и FALSE (ложь). Несмотря на то, что для хранения значений этого типа теоретически достаточно одного бита, обычно в реализациях переменные этого типа занимают один байт памяти. Для всех типов данных, для которых определены операции сравнения, определены также и правила, по которым эти операции сравнения вырабатывают булевские значения. Над булевскими значениями возможны операции конъюнкции (& или AND), дизъюнкции (| или OR) и отрицания (~ или NOT), определяемые следующими таблицами истинности:
TRUE AND TRUE = TRUE
TRUE AND FALSE = FALSE
FALSE AND TRUE = FALSE
FALSE AND FALSE = FALSE
TRUE OR TRUE = TRUE
TRUE OR FALSE = TRUE
FALSE OR TRUE = TRUE
FALSE OR FALSE = FALSE
NOT FALSE = TRUE
NOT TRUE = FALSE При работе с булевскими значениями в языках баз данных некоторую проблему вызывает то, что по причине возможности хранения в базе данных неопределенных значений операции сравнения могут вырабатывать не два, а три логических значения: TRUE, FALSE и UNKNOWN. Поэтому в языке SQL-92, например, используется не двухзначная, а трехзначная логика, в результате чего логические операции при их обработке в серверах баз данных определяются расширенными таблицами (мы приводим их с учетом коммутативности двуместных операций):
TRUE AND TRUE = TRUE
TRUE AND FALSE = FALSE
TRUE AND UNKNOWN = UNKNOWN
FALSE AND UNKNOWN = FALSE
TRUE OR TRUE = TRUE
TRUE OR FALSE = TRUE
TRUE OR UNKNOWN = TRUE
FALSE OR UNKNOWN = UNKNOWN
NOT FALSE = TRUE
NOT TRUE = FALSE
NOT UNKNOWN = UNKNOWN Помимо общего возрастания сложности и недостаточной удовлетворительности трехзначной логики для целей работы с базами данных, неприятность состоит в отсутствии поддержки этой логики в языках программирования (как, впрочем, и в отсутствии явной поддержки неопределенных значений). В языках линии Си прямая поддержка булевского типа данных отсутствует, но имеется логическая интерпретация значений целых типов. Значением операции сравнения может быть "0" (FALSE) или "1" (TRUE). Значение целого типа "0" интерпретируется как FALSE, а значения, отличные от нуля, - как TRUE. В остальном все работает как в случае наличия явной поддержки булевского типа. Тип целых чисел в общем случае включает подмножество целых чисел, определяемое числом разрядов, которое используется для внутреннего представления значений. При определении типа целых чисел обычно стремятся к тому, чтобы множество его значений было симметрично относительно нуля (собственно, это стимулируется и стандартными свойствами машинной целочисленной арифметики). Поэтому приходится тратить один бит на значение знака числа и при использовании n бит для внутреннего представления целого соответствующий тип содержит значения в диапазоне от -2(n-1) до 2(n-1). В подавляющем большинстве современных процессоров отрицательные целые числа обычно представляют в дополнительном коде. В языках, ориентированных на 32-разрядные компьютеры, в частности, в стандартных Си и Си++ для рационального использования памяти допускаются модификации целого типа short integer (обычно 16-разрядные), integer (обычно то же самое, что и long integer) и long integer (обычно 32-разрядные), а также байтовые целые (char). При этом поддерживаются автоматические преобразования значений типов меньшего размера к значениям типов большего размера. Пока не очень понятно, какие встроенные целые типы будут зафиксированы в будущем "64-разрядном" стандарте языка Си, но многие компании считают разумным использовать модель под названием LP64, в которой предполагается размер char - 8 бит, размер short integer - 16 бит, размер integer - 32 бита и размер long integer и long long integer - 64 бита. Наряду со знаковыми целыми типами в языках часто поддерживаются беззнаковые целые.
Такие типы в линии языков Паскаль называются CARDINAL, а в линии языков Си именуются путем добавления модификатора unsigned к названию соответствующего целого типа. Таким образом, в последнем случае существуют типы unsigned char, unsigned short integer, unsigned integer и unsigned long integer. Поскольку множество значений типа unsigned в два раза мощнее множества значений соответствующего целого типа, то поддерживается их автоматическое преобразование только к целым типам большего размера. Наконец, для поддержки численных вычислений в языках обычно специфицируется встроенный тип чисел с плавающей точкой с базовым названием REAL или FLOAT. Обычно в описании языков не фиксируется диапазон и точность значений такого типа. Они уточняются в реализации и обычно существенно зависят от особенностей целевого процессора. В языках семейства Си (32-разрядных) специфицированы три разновидности типа чисел с плавающей точкой - float (обычно с размером 16 бит), double float (размером в 32 бит) и long double float (размером 64 бит).
В этой книге содержатся фундаментальные
В этой книге содержатся фундаментальные материалы, связанные с организацией, сортировкой и поиском данных в основной и внешней памяти. Соответствующие знания необходимы программистам всех уровней (от разработчиков простых прикладных программ до создателей сложнейших систем), квалифицированным пользователям программных продуктов, которые хотят хорошо понимать суть происходящего и, конечно, преподавателям разнообразных компьютерных дисциплин и их студентам. Если обратиться к классической литературе, то можно обнаружить два крайних подхода к представлению материала. Некоторые авторы любят излагать материал на высоком теоретическом уровне. Например, для того, чтобы ввести понятие типа данных и предложить классификацию возможных типов, используются развитые механизмы абстрактной алгебры; при описании алгоритмов в обязательном порядке приводятся асимптотические оценки их сложности. Другой подход состоит в максимальном приближении к практике. Обычно выбирается некоторый конкретный язык программирования, и все описываемые структуры данных и алгоритмы представляются на этом языке. Автору книги ближе некоторый компромисс. С одной стороны мы стремимся максимально использовать интуицию читателей, не перегружая их массой возможных теоретических сведений. С другой стороны, не хочется привязываться к конкретным языковым средам, оставляя изложение на умеренно абстрактном уровне с возможностью адаптации предлагаемого материала к разным возникающим на практике ситуациям. Кроме того, стремясь сделать книгу достаточно структурированной, мы разделяем аспекты структур данных, поиска и сортировки в основной (оперативной) памяти и соответствующие аспекты данных во внешней памяти. По мнению автора, такое четкое разделение материалов более полезно для их возможного использования. Книга состоит из пяти основных частей. В первой части обсуждаются типы данных в том смысле, в каком они используются в языках программирования, а также базовые структуры данных в основной памяти - массивы, записи и множества.
Затем рассматриваются методы организации динамических структур основной памяти, которые, как правило, основываются на динамическом распределении памяти и использовании указателей. Важным аспектом современных сред программирования является возможность пользователей определять свои собственные типы данных с произвольно сложной внутренней структурой и соответствующим набором операций. Анализируются такие важные вопросы, как инкапсуляция типа, наследование типов и полиморфизм. В заключение первой части рассматриваются типы и структуры данных, применяемые в наиболее распространенных в настоящее время реляционных базах данных и в перспективных объектно-реляционных базах данных. Для последней категории баз данных приводится классификация используемых типов и структур данных и анализируются основные свойства, характерные для каждой группы. Вторая часть книги посвящена рассмотрению основных методов и алгоритмов, применяемых для сортировки массивов данных в основной памяти. Мы начинаем с наиболее простых и легко реализуемых методов, которые включают сортировку включением, обменную сортировку, сортировку выбором и сортировку слиянием. После этого обсуждаются более быстрые и более сложные алгоритмы: сортировка разделением и сортировка деревом. В заключение части приводится сравнение описанных методов. В третьей части обсуждаются методы и алгоритмы сортировки последовательностей данных (последовательных файлов), располагаемых во внешней памяти (внешняя сортировка). Опять сначала описываются простые и не очень эффективные алгоритмы внешней сортировки простым слиянием и естественным слиянием, а в конце части рассматриваются более быстрые и сложные алгоритмы сбалансированного многопутевого слияния и многофазной сортировки. Четвертая часть книги посвящена методам поиска данных в основной памяти и применяемым для этого вспомогательным структурам данных. Все известные (и более или менее эффективные) методы поиска можно разделить на два класса: методы, основанные на использовании деревьев, и методы, базирующиеся на хэшировании.
В соответствии с этим разделением часть состоит из двух разделов. В первом разделе рассматриваются наиболее известные методы поиска в основной памяти на основе двоичных деревьев общего вида, сбалансированных (АВЛ) деревьев, деревьев оптимального поиска и деревьях цифрового поиска. Второй раздел посвящен методам хэширования для поиска данных в таблицах основной памяти. В начале раздела обсуждаются алгоритмы совершенного хэширования для поиска в статических таблицах. Далее ставится задача поиска в динамически изменяемых таблицах и возникающая в связи с этим проблема коллизий. В заключение раздела обсуждаются известные методы хэширования с разрешением коллизий: линейное зондирование, двойное хэширование и хэширование с использованием цепочек переполнения. В завершающей, пятой части, обсуждаются методы поиска данных во внешней памяти и связанные с этим служебные структуры данных. И в этой области наиболее распространены подходы на основе деревьев и на основе хэширования. Кроме того, в последние годы появились некоторые относительно новые методы поиска, обеспечивающие большую скорость поиска в редко изменяемых наборах данных. Поэтому часть включает три раздела: методы поиска во внешней памяти на основе деревьев, методы, основанные на хэшировании и "новые" методы. Первый раздел начинается с введения в классические B-деревья. На практике гораздо чаще используется усовершенствованный механизм B-деревьев, который получил название B+-деревьев. После описания общей структуры B+-дерева достаточно подробно обсуждаются алгоритмы поиска, вставки и удаления. Далее анализируются разновидности B+-деревьев, используемые для организации индексов в базах данных, в частности, методы компрессии. Наконец, в заключение первого раздела рассматривается еще одно развитие технологии B-деревьев - R-деревья, предназначенные для организации поиска в пространственных базах данных. Вторая часть содержит описание методов и алгоритмов поиска данных во внешней памяти на основе хэширования. Обсуждаются два классических метода - расширяемое хэширование и линейное хэширование.Анализируются перспективы применения этих методов для организации индексов в нетрадиционных базах данных. Наконец, в третьем разделе рассматриваются все чаще используемые методы, оптимизирующие и убыстряющие поиск в сверхбольших и не слишком часто изменяемых базах данных: индексы хэширования и индексы на основе битовых шкал.
Записи
Типы массивов позволяют работать с регулярными структурами данных, каждый элемент которых относится к одному и тому же базовому типу. Существует другая разновидность составных конструируемых типов данных, которые позволяют определять и использовать нерегулярные структуры данных, элементы которых могут относиться к разным встроенным или явно определенным типам данных. Собирательно типы этой разновидности называются типами записи или структурными типами.
К счастью, общее понятие типа записи практически одинаково в сильно и слабо типизированных языках (с некоторыми оговорками, которые мы отложим до раздела, посвященного указателям). Идея состоит в том, что в определении структурного типа перечисляются имена полей записи, и для каждого поля указывается его тип данных. После этого можно определять переменные вновь сконструированного типа и производить доступ к полям переменных. На языке Модула-2 определение структурного типа "комплексные числа" могло бы выглядеть следующим образом: type complex = record re: real; im: real end
Вот аналог этого определения на языке Си: struct complex { float re; float im; }
После этого можно объявить переменную x комплексного типа (var x: complex; или struct complex x;) и обращаться к действительной и мнимой частям x с помощью конструкции x.re (или x.im соответственно). Поскольку размер составного значения структурного типа точно специфицирован, допускается присваивание таких значений, а также функции, вырабатывающие структурные значения и т.п.
Замечание: мы все же вынуждены отметить одну (не связанную с указателями) особенность использования структурных типов в языках линии Си, отражающую, на наш взгляд, слабость типизации. Кроме корректного с точки зрения типизации отдельного определения именованного структурного типа с использованием затем этого имени при объявлении переменных, можно определять безымянный структурный тип с одновременным объявлением переменных. Например, в языке Си допустимы следующие объявления переменных x, y и z: struct { float re; float im; } x, y;
struct { float r; float i; } z;
После этих объявлений понятно, что переменные x и y имеют один и тот же тип и что, в частности, допустимо присваивание x = y. Но чтобы понять, что на самом деле таким же типом обладает и переменная z, приходится решать громоздкую задачу определения структурной эквивалентности типов, возникновения которой обычно стремятся избежать в сильно типизированных языках программирования.
Записи с вариантами
Можно очень коротко охарактеризовать основные возможности, которые обеспечивает механизм записей. Главное - это то, что в одной именованной области памяти можно хранить совокупность разнотипных именованных полей, причем имена этих полей специфицируются один раз при определении структурного типа данных. Понятно, что без записей можно обойтись, но с их использованием удобнее и экономичнее программировать.
Идея, которую мы обсудим в этом разделе, тоже в основном относится к повышению уровня удобств программирования. При реальном программировании достаточно часто возникает желание по-разному интерпретировать содержимое одной и той же области памяти в зависимости от конкретных обстоятельств. Хорошим стилем является использование каждой структурной переменной с некоторым объектом предметной области, к которой относится программа. Поля структуры в этом случае содержат требуемые характеристики объекта. Но любой объект может менять свое состояние и соответственно набор характеристик. Поэтому удобно, продолжая использовать ту же область памяти, иметь возможность понимать ее структуру и содержание таким образом, который согласуется с текущим состоянием объекта.
Понятно, что для того, чтобы получить такую возможность, нужно несколько расширить средства определения структурного типа, введя вариантность соответствующей структуры. Нужно уметь специфицировать все возможные варианты структурной и типовой интерпретации переменных и значений типа записи. Естественно, что любая такая переменная, вне зависимости от ее конкретной интерпретации, будет занимать один и тот же объем памяти, определяемый "максимальным" по размеру вариантом.
Наиболее строгое решение содержится в языках линии Паскаль. В определении всего структурного типа или его завершающей части можно явно указать специальное поле перечисляемого типа (дискриминант), значения которого являются метками соответствующих вариантов типа записи. Для корректного использования переменных такого типа требуется заносить в поле дискриминанта актуальное значение при изменении интерпретации переменной и руководствоваться значением дискриминанта при доступе к содержимому переменной.
Вот пример определения типа записи с вариантами в языке Паскаль:
type person = record lname, fname: alfa; birthday: date; marstatus: (single, married); case sex: (male, female) of male: (weight: real; bearded: boolean); female: (size: array[1..3] of integer) end
(Считается, что типы данных alfa и date уже определены.) После определения переменной типа person в любой момент можно обращаться и к полям weight и bearded, и к элементам массива size, но корректно это следует делать, руководствуясь значением дискриминанта sex. Более слабый, но эквивалентный по возможностям механизм поддерживается в языках семейства Си. В этих языках существует специальная разновидность типов данных, называемая смесью (union). Фактически, смесь - это запись с вариантами, но без явно поддерживаемого дискриминанта. По нашему мнению, решение о применении такого "облегченного" механизма было принято потому, что использование явно задаваемого дискриминанта в языках линии Паскаль все равно является необязательным, а раз так, то при желании можно просто включить дополнительное поле, значение которого будет характеризовать применимый вариант. Приведенный выше пример можно было бы переписать на языке Си следующим образом:
struct person { char lname[10], fname[10]; integer birthday; enum { single, married } marstatus; enum { male, female } sex; union { struct { float weight; integer bearded } male; integer female[3]; } pers; }
