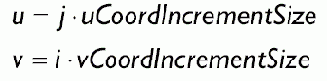Введение в программирование трехмерных игр с DX9
         

Сетка с треугольными ячейками



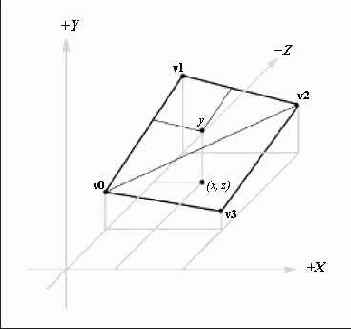
Рисунок 13.1. (a) Сетка с треугольными ячейками. (б) Сетка с плавным изменением высот. (в) Освещенный и текстурированный ландшафт, который будет формировать пример приложния, создаваемый в данной главе


Эта глава познакомит вас с реализацией класса Terrain, использующим метод грубой силы. Под этим подразумевается, что он просто хранит данные вершин и индексов для всего ландшафта и визуализирует их. Для игр с ландшафтом небольшого размера такой подход работает, при том условии, что в компьютере установлена современная видеокарта поддерживающая аппаратную обработку вершин. Однако для тех игр, которым требуется большой ландшафт, мы должны выполнить дополнительную работу по изменению уровня детализации или отбрасыванию невидимых граней, поскольку при использовании метода грубой силы огромное количество геометрических данных, необходимых для моделирования обширных ландшафтов приведет к перегрузке видеокарты.

Цели

Узнать как генерируется информация о высотах ландшафта, обеспечивающая плавный переход от гор к долинам, подобный природным ландшафтам.

Изучить способы генерации данных о вершинах и треугольных гранях ландшафта.

Познакомиться с техникой, применяемой для освещения и текстурирования ландшафта.

Изучить способ перемещения камеры по ландшафту, чтобы создавалось впечатление ходьбы или бега.



Вычисляем два вектора, совпадающих



Рисунок 13.12. (а) Вычисляем два вектора, совпадающих со сторонами треугольника. (б) Высота вычисляется путем линейной интерполяции u на dx и v на dz


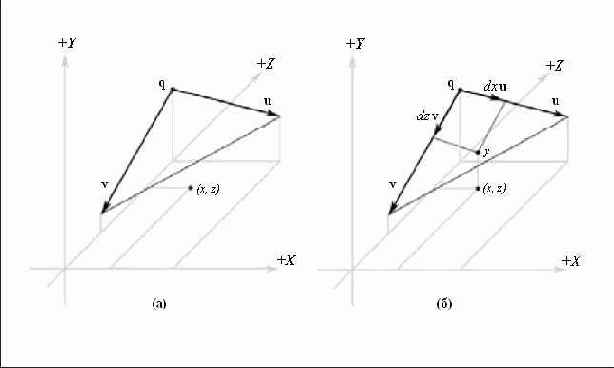
Обратите внимание, что поскольку нас интересует только значение высоты, мы можем выполнять интерполяцию только для компоненты y и игнорировать остальные компоненты. В этом случае высота определяется по формуле A + dxuy + dzvy.

Итак, вот заключительная часть кода метода Terrian::getHeight:

if(dz < 1.0f - dx) // верхний треугольник ABC { float uy = B - A; // A->B float vy = C - A; // A->C

height = A + d3d::Lerp(0.0f, uy, dx) + d3d::Lerp(0.0f, vy, dz); } else // нижний треугольник DCB { float uy = C - D; // D->C float vy = B - D; // D->B

height = D + d3d::Lerp(0.0f, uy, 1.0f - dx) + d3d::Lerp(0.0f, vy, 1.0f - dz); } return height; }

Функция Lerp выполняет линейную интерполяцию вдоль одномерной линии и ее реализация выглядит так:

float d3d::Lerp(float a, float b, float t) { return a - (a*t) + (b*t); }





Досуп к карте высот и ее модификация



13.1.3. Досуп к карте высот и ее модификация

Для доступа к элементам карты высот и их модификации класс Terrain предоставляет следующие два метода:

int Terrain::getHeightmapEntry(int row, int col) { return _heightmap[row * _numVertsPerRow + col]; }

void Terrain::setHeightmapEntry(int row, int col, int value) { _heightmap[row * _numVertsPerRow + col] = value; }

Эти методы позволяют ссылаться на элемент карты, указывая номера строки и столбца, и скрывают выполняемое преобразование в индекс одномерного массива.



Основы визуализации ландшафтов


Сетка ландшафта представляет собой обычную сетку с треугольными ячейками, подобную показанной на Рисунок 13.1(а), у которой для каждой вершины сетки высота задана таким образом, чтобы сетка моделировала плавный переход от гор к долинам, подобный природному ландшафту (Рисунок  13.1(б)). И, конечно же, мы накладываем тщательно подобранные текстуры, изображающие песчанные пляжи, покрытые травой склоны и заснеженные вершины (Рисунок  13.1(в)).



«Ходьба» по ландшафту


После того, как мы сконструировали ландшафт, хорошо добавить возможность перемещать камеру таким образом, чтобы она имитировала ходьбу по ландшафту. То есть нам надо менять высоту камеры (координату Y) в зависимости от того, в каком месте ландшафта мы находимся. Для этого мы сначала должны определить по координатам X и Z камеры квадрат ландшафта в котором мы находимся. Все это делает функция Terrain::getHeight; в своих параметрах она получает координаты X и Z камеры и возвращает высоту, на которой должна быть расположена камера, чтобы она оказалась над ландшафтом. Давайте рассмотрим реализацию функции.

float Terrain::getHeight(float x, float z) { // Выполняем преобразование перемещения для плоскости XZ, // чтобы точка START ландшафта совпала с началом координат. x = ((float)_width / 2.0f) + x; z = ((float)_depth / 2.0f) - z;

// Масштабируем сетку таким образом, чтобы размер // каждой ее ячейки стал равен 1. Для этого используем // коэффициент 1 / cellspacing поскольку // cellspacing * 1 / cellspacing = 1. x /= (float)_cellSpacing; z /= (float)_cellSpacing;

Сперва мы выполняем перемещение в результате которого начальная точка ландшафта будет совпадать с началом координат. Затем мы выполняем операцию масштабирования с коэффициентом равным единице деленной на размер клетки; в результате размер клетки ландшафта будет равен 1. Затем мы переходим к новой системе координат, где положительное направление оси Z направлено «вниз». Конечно, вы не найдете кода меняющего систему координат, просто помните, что ось Z направлена вниз. Все эти этапы показаны на Рисунок 13.9.



Исходная сетка ландшафта и сетка



Рисунок 13.9. Исходная сетка ландшафта и сетка после переноса начальной точки ландшафта в начало координат, масштабирования, делающего размер квадрата равным 1 и смены направления оси Z


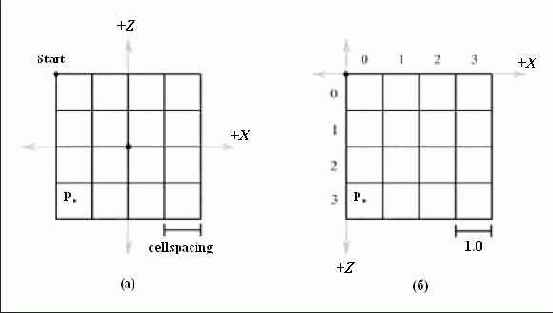
Мы видим, что измененная координатная система соответствует порядку элементов матрицы. То есть верхний левый угол — это начало координат, номера столбцов увеличиваются вправо, а номера строк растут вниз. Следовательно, согласно рис 13.9, и помня о том, что размер ячейки равен 1, мы сразу видим что номер строки и столбца для той клетки на которой мы находимся вычисляется так:

float col = ::floorf(x); float row = ::floorf(z);

Другими словами, номер столбца равен целой части координаты X, а номер строки — целой части координаты Z. Также вспомните, что результатом функции floor(t) является наибольшее целое число, которое меньше или равно t.

Теперь, когда мы знаем в какой ячейке находимся, можно получить высоты ее четырех вершин:

// A B // *---* // | / | // *---* // C D float A = getHeightmapEntry(row, col); float B = getHeightmapEntry(row, col+1); float C = getHeightmapEntry(row+1, col); float D = getHeightmapEntry(row+1, col+1);

Теперь мы знаем в какой ячейке находимся и высоты всех четырех ее вершин. Нам надо найти высоту (координату Y) точки ячейки с указанными координатами X и Z, где находится камера. Это нетривиальная задача, поскольку ячейка может быть наклонена, как показано на Рисунок  13.10.



Карты высот


Мы используем карты высот, чтобы указать, где на нашем ландшафте находятся горы, а где— долины. Карта высот (heighmap) — это массив, в котором каждый элемент задает высоту отдельной вершины сетки ландшафта. (Существует и альтернативная реализация, в которой элемент карты высот соответствует квадрату ландшафта.) Обычно мы представляем карту высот в виде матрицы, каждый элемент которой однозначно соответствует вершине сетки ландшафта.

Когда мы сохраняем карту высот на диске, для каждого ее элемента обычно отводится один байт, так что значения высоты могут находиться в диапазоне от 0 до 255. Хотя диапазон от 0 до 255 достаточен для хранения перепадов высот нашего ландшафта, в приложении может потребоваться масштабирование этого значения, чтобы оно соответствовало масштабу нашего трехмерного мира. Предположим, что в качестве единиц измерения для нашего трехмерного мира мы выбрали сантиметры, тогда диапазона значений от 0 до 255 будет недостаточно, чтобы изобразить что-нибудь интересное. Поэтому при загрузке данных в приложение мы выделяем для каждого элемента карты высот переменную типа int или float. Это позволяет масштабировать значения за пределы диапазона от 0 до 255, чтобы они соответствовали любому требуемому масштабу.

Одним из возможных представлений карты высот является карта с градациями серого, где темные области соответствуют низинам, а светлые — возвышенностям. Такая карта показана на Рисунок  13.2.



Мы можем моделировать ландшафты используя


Мы можем моделировать ландшафты используя сетку с треугольными ячейками, вершинам которой присвоены различные высоты для создания возвышенностей и низин, имитирующих ландшафт.
Карта высот — это набор данных, содержащий значения высот для каждой вершины ландшафта.
Мы можем текстурировать ландшафт, используя в качестве текстуры хранящееся на диске изображение, либо создавая текстуру программно.
Мы освещаем ландшафт путем вычисления коэффициента затенения для каждого квадрата, определяющего насколько светлым или темным должен быть квадрат. Коэффициент затенения зависит от угла под которым свет падает на квадрат.
Чтобы камера имитировала «ходьбу» по ландшафту нам нужно уметь определять на каком треугольнике сетки ландшафта мы находимся в данный момент. После этого мы формируем два вектора, совпадающих со сторонами этого треугольника. После этого высота определяется путем линейной интерполяции этих векторов с использованием координат по осям X и Z в нормализованной ячейке ландшафта, начало которой совпадает с началом координат, а размеры сторон равны единице.

Ячейка до и после преобразования, переносящего ее верхнюю левую вершину в начало координат



Рисунок 13.11. Ячейка до и после преобразования, переносящего ее верхнюю левую вершину в начало координат


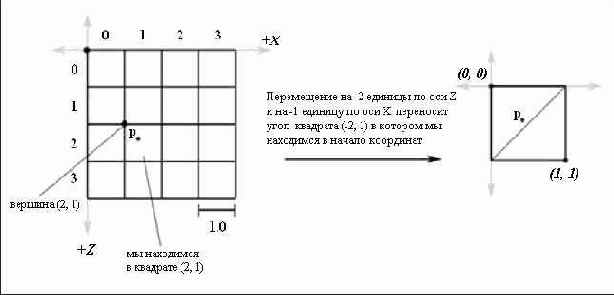Теперь, если dz < 1.0 – dx мы находимся в «верхнем» треугольнике Δv0v1v2. В ином случае мы находимся в «нижнем» треугольнике Δv0v2v3 (Рисунок  13.10).

Теперь мы посмотрим как определить высоту, если мы находимся в «верхнем» треугольнике. Для «нижнего» треугольника процесс аналогичен и ниже будет приведен код для обоих вариантов. Чтобы найти высоту когда мы находимся в «верхнем» треугольнике, надо сформировать два вектора u = (cellSpacing, B – A, 0) и v = (0, C – A, –cellSpacing), совпадающих со сторонами треугольника и начинающихся в точке, заданной вектором q = (qx, A, qz), как показано на Рисунок  13.12(а) Затем мы выполняем линейную интерполяцию вдоль вектора u на dx и вдоль вектора v на dz. Эти интерполяции показаны на Рисунок  13.12(б). Координата Y вектора (q + dxu + dzv) дает нам высоту для заданных координат X и Z; чтобы увидеть, как это происходит, вспомните геометрическую интерпретацию сложения векторов.



Карта градаций серого, созднная в Adobe Photoshop


Рисунок 13.3. Карта градаций серого, созднная в Adobe Photoshop


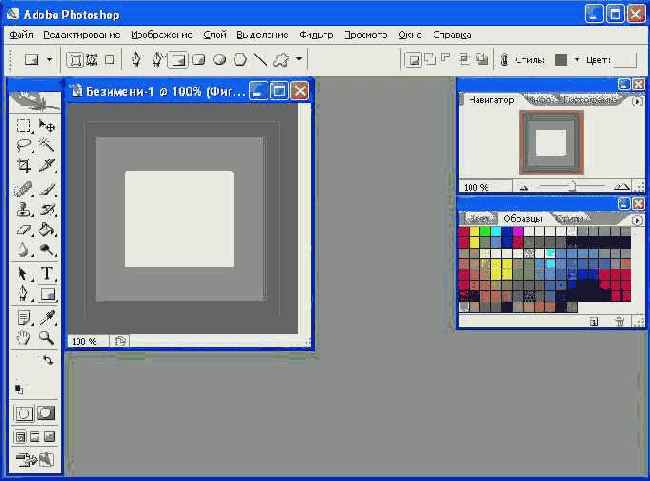Когда вы завершите рисование своей карты высот, сохраните ее как 8-разрядный файл RAW. Файлы RAW просто содержат байты изображения один за другим. Благодаря этому чтение данных изображения в приложении выполняется очень просто. Ваш графический редактор может спростить, сохранять ли изображение в файл RAW с заголовком. Укажите, что заголовок не нужен.

ПРИМЕЧАНИЕ

Вы не обязаны использовать для хранения информации о высотах формат RAW; применяйте любой формат, соответствующий вашим потребностям. Формат RAW — это только один пример формата, который можно использовать. Мы выбрали его по той причине, что большинство популярных графических редакторов могут выполнять экспорт изображения в этот формат и чтение данных из файла RAW в приложении реализуется очень просто. В примерах из этой главы используются 8-разрядные файлы RAW.

Затем для каждого квадрата ландшафта мы вычисляем угол между вектором освещения



Освещение


Метод Terrain::genTexture обращается к функции Terrain::lightTerrain, которая, как говорит ее имя, выполняет освещение ландшафта для увеличения реализма сцены. Поскольку мы уже вычислили цвета текстуры ландшафта, нам осталось вычислить только коэффициент затенения, который делает отдельные участки темнее или светлее в зависимости от их расположения относительно источника света. В данном разделе мы исследуем такую технику. Вы можете недоумевать, почему мы занялись освещением ландшафта, а не позволили Direct3D все сделать за нас. У самостоятельного выполнения вычислений есть три преимущества:

Мы экономим память, поскольку нам не надо хранить нормали вершин.

Так как ландшафты статичны и мы не будем перемещать источники света, можно заранее рассчитать освещение, освободив то время, которое Direct3D тратил бы на расчет освещения ландшафта в реальном времени.

Мы попрактикуемся в математике, познакомимся с базовыми концепциями освещения и поработаем с функциями Direct3D.



Пример приложения: ландшафт


Пример приложения для этой главы создает ландшафт на основе содержащихся в файле RAW данных карты высот, текстурирует его и рассчитывает освещение. Помимо этого, с помощью клавиш управления курсором можно перемещаться по ландшафту. Обратите внимание, что в приведенных ниже фрагментах не относящийся к рассматриваемой теме код пропущен; места, где должен находиться пропущенный код отмечены многоточиями. Имейте в виду, что скорость работы приложения зависит от установленного оборудования; если программа работает медленно, попробуйте уменьшить размер ландшафта.

Сперва мы добавляем глобальные переменные, представляющие наш ландшафт, камеру и счетчик частоты кадров:

Terrain* TheTerrain = 0; Camera TheCamera(Camera::LANDOBJECT);

FPSCounter* FPS = 0;

Теперь посмотрите на функции каркаса приложения:

bool Setup() { D3DXVECTOR3 lightDirection(0.0f, -1.0f, 0.0f); TheTerrain = new Terrain(Device, "coastMountain256.raw", 256, 256, 10, 1.0f); TheTerrain->genTexture(); TheTerrain->lightTerrain(&directionToLight);

...

return true; }

void Cleanup() { d3d::Delete<Terrain*>(TheTerrain); d3d::Delete<FPSCounter*>(FPS); }

bool Display(float timeDelta) { if( Device ) { // // Обновление сцены: //

...[пропущен код для проверки ввода]

// Ходьба по ландшафту: настраиваем высоту // камеры таким образом, чтобы она находилась // в 5 единицах над поверхностью той ячейки, // где мы находимся. D3DXVECTOR3 pos; TheCamera.getPosition(&pos);

float height = TheTerrain->getHeight(pos.x, pos.z);

pos.y = height + 5.0f;

TheCamera.setPosition(&pos);

D3DXMATRIX V; TheCamera.getViewMatrix(&V); Device->SetTransform(D3DTS_VIEW, &V);

// // Рисование сцены: // Device->Clear(0, 0, D3DCLEAR_TARGET | D3DCLEAR_ZBUFFER, 0xff000000, 1.0f, 0); Device->BeginScene();

D3DXMATRIX I; D3DXMatrixIdentity(&I);

if(TheTerrain) TheTerrain->draw(&I, false);

if(FPS) FPS->render(0xffffffff, timeDelta);

Device->EndScene(); Device->Present(0, 0, 0, 0); } return true; }



Процедурный подход



13.3.1. Процедурный подход

Альтернативным способом текстурирования ландшафта является программное вычисление текстуры; это означает, что мы создаем «пустую» текстуру и вычисляем цвет каждого ее текселя в коде на основании некоторых предопределенных параметров. В нашем примере таким параметром является высота вершины ландшафта.

Программная генерация текстуры выполняется в методе Terrain::genTexture. Сперва мы создаем пустую текстуру с помощью метода D3DXCreateTexture. Затем мы блокируем текстуру верхнего уровня (помните, что это детализируемая текстура и у нее есть несколько уровней детализации). После этого мы в цикле перебираем тексели и назначаем их цвет. Цвета текселей зависят от высоты вершин квадрата сетки, которому они принадлежат. Идея заключается в том, что низкие участки ландшафта окрашиваются в цвет песчанного пляжа, участки со средней высотой — в цвет травы, а высокие части ландшафта — в цвет снежных вершин. Мы считаем, что высота квадрата это высота его верхнего левого угла.

Назначив цвета всем текселям, мы должны сделать некоторые из них темнее или светлее в зависимости от того, под каким углом солнечный свет (моделируемый с помощью источника направленного света) падает на квадрат ландщафта, соответствующий данному текселю. Все это делается в методе Terrain::lightTerrain, реализация которого будет обсуждаться в следующием разделе.

В конце метода Terrain::genTexture осуществляется вычисление текселей остальных уровней детализируемой текстуры. Это делается с помощью функции D3DXFilterTexture. Вот как выглядит код генерации текстуры:

bool Terrain::genTexture(D3DXVECTOR3* directionToLight) { // Метод программно заполняет текстуру верхнего уровня. // Затем выполняется ее освещение. И, в конце, заполняются // остальные уровни детализируемой текстуры с помощью // D3DXFilterTexture.

HRESULT hr = 0;

// Тексель для каждого квадрата сетки int texWidth = _numCellsPerRow; int texHeight = _numCellsPerCol;

// Создаем пустую текстуру hr = D3DXCreateTexture( _device, texWidth, texHeight, // размеры 0, // создаем полную // цепочку детализации 0, // использование - нет D3DFMT_X8R8G8B8, // формат 32-разрядный XRGB D3DPOOL_MANAGED, // пул памяти &_tex);


if(FAILED(hr)) return false;

D3DSURFACE_DESC textureDesc; _tex->GetLevelDesc(0 /* уровень */, &textureDesc);

// Проверяем, что получена текстура требуемого формата, // поскольку наш код заполнения текстуры работает только // с 32-разрядными пикселями if(textureDesc.Format != D3DFMT_X8R8G8B8) return false;

D3DLOCKED_RECT lockedRect; _tex->LockRect(0, // блокируем верхнюю поверхность &lockedRect, 0, // блокируем всю текстуру 0); // флаги

// Заполняем текстуру DWORD* imageData = (DWORD*)lockedRect.pBits; for(int i = 0; i < texHeight; i++) { for(int j = 0; j < texWidth; j++) { D3DXCOLOR c; // Получаем высоту верхней левой вершины квадрата float height = (float)getHeightmapEntry(i, j)/_heightScale;

// Устанавливаем цвет текселя на основе высоты // соответствующего ему квадрата if( (height) < 42.5f ) c = d3d::BEACH_SAND; else if( (height) < 85.0f ) c = d3d::LIGHT_YELLOW_GREEN; else if( (height) < 127.5f ) c = d3d::PUREGREEN; else if( (height) < 170.0f ) c = d3d::DARK_YELLOW_GREEN; else if( (height) < 212.5f ) c = d3d::DARKBROWN; else c = d3d::WHITE;

// Заполняем заблокированный буфер. Обратите внимание, что мы // делим шаг на четыре, поскольку шаг измеряется в байтах // а одно значение DWORD занимает 4 байта imageData[i * lockedRect.Pitch / 4 + j] = (D3DCOLOR)c; } } _tex->UnlockRect(0);

// Освещаем ландшафт if(!lightTerrain(directionToLight)) { ::MessageBox(0, "lightTerrain() - FAILED", 0, 0); return false; }

// Заподняем цепочку детализации hr = D3DXFilterTexture( _tex, // текстура, для которой заполняются уровни детализации 0, // палитра по умолчанию 0, // используем в качестве источника верхний уровень D3DX_DEFAULT); // фильтр по умолчанию

if(FAILED(hr)) { ::MessageBox(0, "D3DXFilterTexture() - FAILED", 0, 0); return false; } return true; }

Обратите внимание, что константы цветов, BEACH_SAND и т.п., определены в файле d3dUtility.h.


Соответствие между вершинами ландшафта и координатами текстур



Рисунок 13.5. Соответствие между вершинами ландшафта и координатами текстур



Обзор


13.4.1. Обзор

Техника освещения, которую мы будем использовать для вычисления оттенков ландшафта является одной из самых простых и известна как рассеянное освещение (diffuse lighting). Мы используем параллельный источник света, который описываем путем указания направления на источник света, являющегося противоположным тому направлению, в котором падают испускаемые источником лучи. Например, если мы хотим чтобы лучи света падали с неба вертикально вниз в направлении lightRaysDirection= (0, –1, 0), то направлением на источник света будет указывающий в противоположном направлении вектор directionToLight = (0, 1, 0). Обратите внимание, что мы используем единичные векторы.

ПРИМЕЧАНИЕ

Хотя указание направления испускаемых источником света лучей может казаться более интуитивно понятным, задание направления на источник света больше подходит для вычисления рассеянного освещения.
<
И, в заключение, приведем код генерации данных вершин:

bool Terrain::computeVertices() { HRESULT hr = 0;

hr = _device->CreateVertexBuffer( _numVertices * sizeof(TerrainVertex), D3DUSAGE_WRITEONLY, TerrainVertex::FVF, D3DPOOL_MANAGED, &_vb, 0);

if(FAILED(hr)) return false;

// координаты, с которых начинается генерация вершин int startX = -_width / 2; int startZ = _depth / 2;

// координаты, на которых завершается генерация вершин int endX = _width / 2; int endZ = -_depth / 2;

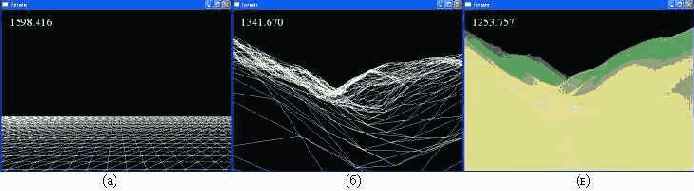
// вычисляем приращение координат текстуры // при переходе от одной вершины к другой. float uCoordIncrementSize = 1.0f / (float)_numCellsPerRow; float vCoordIncrementSize = 1.0f / (float)_numCellsPerCol;

TerrainVertex* v = 0; _vb->Lock(0, 0, (void**)&v, 0);

int i = 0; for(int z = startZ; z >= endZ; z -= _cellSpacing) { int j = 0; for(int x = startX; x <= endX; x += _cellSpacing) { // вычисляем правильный индекс в буфере вершин // и карте высот на основании счетчиков вложенных циклов int index = i * _numVertsPerRow + j;

v[index] = TerrainVertex( (float)x, (float)_heightmap[index], (float)z, (float)j * uCoordIncrementSize, (float)i * vCoordIncrementSize);

j++; // следующий столбец } i++; // следующая строка }

_vb->Unlock();

return true; }


Создание карты высот



13.1.1. Создание карты высот

Карта высот может быть создана либо программно, либо с помощью графического редактора, например Adobe Photoshop. Использование графического редактора— более простой способ, позволяющий интерактивно создавать ландшафты и видеть полученный результат. Кроме того, можно создавать необычные карты высот, пользуясь дополнительными возможностями графического редактора, такими как фильтры. На Рисунок  13.3 показана пирамидальная карта высот, созданная в Adobe Photoshop с помощью инструментов редактирования. Обратите внимание, что при создании изображения мы выбираем карту градаций серого.



Свойства размеченной треугольной сетки Точки на пересечении линий сетки обозначают вершины



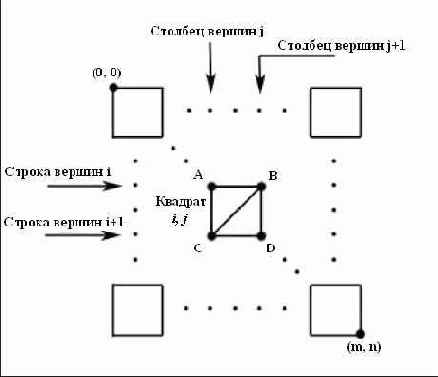
Рисунок 13.4. Свойства размеченной треугольной сетки. Точки на пересечении линий сетки обозначают вершины

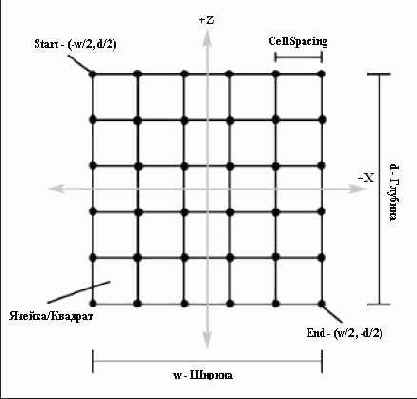
Рисунок 13.4 иллюстрирует свойства ландшафта, термины и специальные точки, на которые мы будем ссылаться. Размер ландшафта определяется путем указания количества вершин в строке, количества вершин в столбце и размера ячейки. Все эти значения мы передаем в класс Terrain. Кроме того, мы передаем указатель на связанное с ландшафтом устройство, строку с именем файла, содержащего карту высот и коэффициент масштабирования, используемый при масштабировании элементов карты высот.

class Terrain { public: Terrain( IDirect3DDevice9* device, std::string heightmapFileName, int numVertsPerRow, int numVertsPerCol, int cellSpacing, // расстояние между вершинами float heightScale); // коэффициент масштабирования высоты

... методы пропущены

private: ...устройство, буфер вершин и т.п. пропущены

int _numVertsPerRow; int _numVertsPerCol; int _cellSpacing; int _numCellsPerRow; int _numCellsPerCol; int _width; int _depth; int _numVertices; int _numTriangles; float _heightScale; };

Чтобы увидеть объявление класса Terrain полностью, посмотрите исходный код примера в сопроводительных файлах; оно слишком велико, чтобы приводить его в тексте.

На основании переданных конструктору данных мы вычисляем другие параметры ландшафта:

_numCellsPerRow = _numVertsPerRow - 1; _numCellsPerCol = _numVertsPerCol - 1; _width = _numCellsPerRow * _cellSpacing; _depth = _numCellsPerCol * _cellSpacing; _numVertices = _numVertsPerRow * _numVertsPerCol; _numTriangles = _numCellsPerRow * _numCellsPerCol * 2;

Кроме того, мы объявляем структуру вершин ландшафта следующим образом:

struct TerrainVertex { TerrainVertex(){} TerrainVertex(float x, float y, float z, float u, float v) { _x = x; _y = y; _z = z; _u = u; _v = v; } float _x, _y, _z; float _u, _v;

static const DWORD FVF; }; const DWORD Terrain::TerrainVertex::FVF = D3DFVF_XYZ | D3DFVF_TEX1;

Обратите внимание, что TerrainVertex — это вложенный класс, объявленный внутри класса Terrain. Мы выбрали такую реализацию по той причине, что класс TerrainVertex не нужен вне класса Terrain.



Текстурирование


Класс Terrain предоставляет два способа текстурирования ландшафта. Наиболее очевидный способ— загрузить ранее подготовленную текстуру из файла и использовать ее. Показанный ниже метод, реализованный в классе Terrain, загружает текстуру из файла в член данных _tex, являющийся указателем на интерфейс IDirect3DTexture9. Внутри метода Terrain::draw перед визуализацией ландшафта устанавливается текстура _tex.

Если вы прочитали предыдущие главы, реализация метода не должна вызвать у вас никаких вопросов.

bool Terrain::loadTexture(std::string fileName) { HRESULT hr = 0;

hr = D3DXCreateTextureFromFile( _device, fileName.c_str(), &_tex);

if(FAILED(hr)) return false;

return true; }



Угол между вектором освещения



Рисунок 13.7. Угол между вектором освещения

и нормалью поверхности
определяет сколько света получает поверхность. На рисунке (a) угол меньше 90 градусов. На рисунке (б) угол больше 90 градусов. Заметьте, что во втором случае поверхность не получает света потому что лучи света (испускаемые в направлении противоположном вектору
) попадают на обратную сторону поверхности

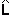
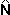
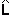
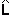
Используя угловые отношения между вектором освещения и нормалю поверхности можно вычислить коэффициент затенения, находящийся в диапазоне [0, 1], который определяет сколько света получает поверхность. Большие углы представляются близкими к нулю значениями коэффициента. Когда цвет умножается на близкий к нулю коэффициент затенения, он становится темнее, а это именно то, что нам надо. С другой стороны, малые углы представляются близкими к единице значениями коэффициента, и умножение на этот коэффициент практически не меняет яркость цвета.



Вершины квадрата



Рисунок 13.6. Вершины квадрата

<
Главным трюком здесь является общая формула, позволяющая вычислить индексы треугольников, образующих квадрат в позиции (i, j). Рисунок  13.6 позволяет вывести общую формулу для квадрата(i, j):

ΔABC = { i*numVertsPerRow + j, i*numVertsPerRow + j + 1, (i + 1)*numVertsPerRow + j }

ΔCBD = { (i + 1)*numVertsPerRow + j, i*numVertsPerRow + j + 1, (i + 1)*numVertsPerRow + j + 1 }

Вот код генерации индексов:

bool Terrain::computeIndices() { HRESULT hr = 0;

hr = _device->CreateIndexBuffer( _numTriangles * 3 * sizeof(WORD), // 3 индекса на треугольник D3DUSAGE_WRITEONLY, D3DFMT_INDEX16, D3DPOOL_MANAGED, &_ib, 0);

if(FAILED(hr)) return false;

WORD* indices = 0; _ib->Lock(0, 0, (void**)&indices, 0);

// Индекс, с которого начинается группа из 6 индексов, // описывающая два треугольника, образующих квадрат int baseIndex = 0;

// В цикле вычисляем треугольники для каждого квадрата for(int i = 0; i < _numCellsPerCol; i++) { for(int j = 0; j < _numCellsPerRow; j++) { indices[baseIndex] = i * _numVertsPerRow + j; indices[baseIndex + 1] = i * _numVertsPerRow + j + 1; indices[baseIndex + 2] = (i+1) * _numVertsPerRow + j; indices[baseIndex + 3] = (i+1) * _numVertsPerRow + j; indices[baseIndex + 4] = i * _numVertsPerRow + j + 1; indices[baseIndex + 5] = (i+1) * _numVertsPerRow + j + 1;

// следующий квадрат baseIndex += 6; } }

_ib->Unlock();

return true; }


Возможные усовершенствования


Рассмотренная реализация класса Terrain загружает данные всех вершин ландшафта в один огромный буфер вершин. С точки зрения скорости и масштабируемости было бы хорошо разделить геометрию ландшафта на несколько буферов вершин. Возникает вопрос: «Какой размер буфера лучше выбрать?». Ответ зависит от конфигурации аппаратуры компьютера. Так что экспериментируйте!

Поскольку деление геометрии ландшафта на несколько небольших буферов вершин в основном связано с индексацией в подобной матрице структуре данных и управленим данными, а также не вносит никаких новых концепций, мы не станем подробно обсуждать его. Если коротко, вы делите ландшафт на матрицу элементов, которые мы будем называть «блоки». Каждый блок охватывает прямоугольный фрагмент ландшафта и содержит описание геометрии этого фрагмента (в собственных буферах вершин и индексов). Следовательно, каждый блок отвечает за рисование той части ландшафта, данные которой он содержит.

Альтернативным способом является загрузка всей геометрии ландшафта в один большой экземпляр интерфейса ID3DXMesh. Затем для разделения сетки ландшафта на несколько меньших используется функция D3DXSplitMesh из библиотеки D3DX. Прототип функции D3DXSplitMesh выглядит так:

void D3DXSplitMesh( const LPD3DXMESH pMeshIn, const DWORD *pAdjacencyIn, const DWORD MaxSize, const DWORD Options, DWORD *pMeshesOut, LPD3DXBUFFER *ppMeshArrayOut, LPD3DXBUFFER *ppAdjacencyArrayOut, LPD3DXBUFFER *ppFaceRemapArrayOut, LPD3DXBUFFER *ppVertRemapArrayOut );

Эта функция получает исходную сетку и делит ее на несколько меньших. Параметр pMeshIn — это указатель на сетку, которую мы хотим разделить, а pAdjacencyIn — это указатель на массив данных о смежности для этой сетки. Параметр MaxSize используется для указания максимального количества вершин в получаемых в результате разделения фрагментах сетки. Набор флагов Options задает параметры создания для формируемых сеток-фрагментов. Через параметр pMeshesOut возвращается количество полученных фрагментов, а сами фрагменты возвращаются в массиве буферов ppMeshArrayOut. Последние три параметра — необязательные (чтобы игнорировать их укажите null) и возвращают массивы данных о смежности и информацию о перемещении граней и вершин для каждой из созданных сеток.



Вычисление двух векторов, находящихся в одной плоскости с квадратом



Рисунок 13.8. Вычисление двух векторов, находящихся в одной плоскости с квадратом



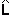
Вычисление индексов— определение треугольников



13.2.2. Вычисление индексов — определение треугольников

Чтобы вычислить индексы сетки мы просто в цикле перебираем все ее квадраты, начиная с верхнего левого и заканчивая правым нижним, как показано на Рисунок  13.4, и формируем два треугольника, образующие квадрат.

При вычислении координат текстуры, учитывая Рисунок  13.5, получаем простой сценарий, определяющий соответствие координат текстуры (u, v) вершине ландшафта (i, j) по следующей формуле:



Вычисление затенения квадрата



13.4.2. Вычисление затенения квадрата

Направление на источник света нам дано в виде нормализованного вектора



Высота ячейки (координата Y) для заданных координат местоположения камеры X и Z



Рисунок 13.10. Высота ячейки (координата Y) для заданных координат местоположения камеры X и Z



Вычисление вершин


13.2.1. Вычисление вершин

Во время последующего обсуждения смотрите на Рисунок  13.4. Чтобы создать вершины нашей сетки мы просто начинаем генерировать данные вершин с той, которая отмечена на рисунке словом start и заполняем вершины ряд за рядом, пока не дойдем до той, которая отмечена словом end; при этом расстояние между вершинами задается параметром cellSpacing. Это позволяет нам получить координаты X и Z, но как насчет координаты Y? Координата Y берется из соответствующего элемента загруженной карты высот.

ПРИМЕЧАНИЕ

Рассматриваемая реализация использует один большой буфер вершин для хранения данных всех вершин всего ландшафта. Это может вызвать проблемы, связанные с накладываемым оборудованием ограничениями. Например, параметры устройства задают максимальное количество примитивов и максимальное количество индексов вершин. Проверьте значения членов MaxPrimitiveCount и MaxVertexIndex структуры D3DCAPS9, чтобы увидеть какие ограничения накладывает используемое вами оборудование. Решение проблем ,вызванных использованием одного буфера вершин, обсуждается в разделе 13.7.

Чтобы определить высоту мы должны узнать в каком треугольнике ячейки мы находимся. Вспомните, что каждая ячейка визуализируется как два треугольника. Чтобы определить в каком треугольнике мы находимся, мы берем тот квадрат сетки в котором находимся и перемещаем его таким образом, чтобы верхняя левая вершина совпадала с началом координат.

Поскольку переменные row и col определяют местоположение левой верхней вершины той ячейки где мы находимся, необходимо выполнить перемещение на –col по оси X и –row по оси Z. Преобразование координат X и Z выполняется так:

float dx = x - col; float dz = z - row;

Ячейка после выполнения преобразования показана на Рисунок 13.11.



Загрузка файла RAW



13.1.2. Загрузка файла RAW

Поскольку файл RAW— это всего лишь непрерывный массив байтов, мы можем просто прочитать его целиком с помощью приведенного ниже метода. Обратите внимание, что переменная _heightmap — это член класса Terrain, определеный следующим образом: std::vector<int> _heightmap;.

bool Terrain::readRawFile(std::string fileName) { // Высота для каждой вершины std::vector<BYTE> in(_numVertices);

std::ifstream inFile(fileName.c_str(), std::ios_base::binary);

if(inFile == 0) return false;

inFile.read( (char*)&in[0], // буффер in.size()); // количество читаемых в буфер байт

inFile.close();

// копируем вектор BYTE в вектор int _heightmap.resize(_numVertices); for(int i = 0; i < in.size(); i++) _heightmap[i] = in[i];

return true; }

Обратите внимание, что мы копируем вектор байтов в вектор целых чисел; это делается для того, чтобы потом мы могли масштабировать значения высот для выхода за пределы диапазона [0, 255].

Единственным ограничением данного метода является то, что количество байт в читаемом файле RAW должно быть не меньше количества вершин в сетке ландшафта. Следовательно, если вы считываете файл RAW размером 256 × 256, то должны создать ландшафт в котором будет не более 256 × 256 вершин.



Затенение ландшафта



13.4.3. Затенение ландшафта

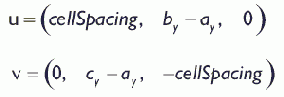
Теперь, когда мы узнали как выполнить затенение отдельного квадрата, можно выполнить затенение всех квадратов ландшафта. Мы просто перебираем в цикле все квадраты ландшафта, вычисляем для каждого из них коэффициент затенения и умножаем цвет соответствующего квадрату текселя на полученный коэффициент. В результате квадраты, получающие мало света станут темнее. Ниже приведен фрагмент кода, являющийся главной частью метода Terrain::lightTerrain:

DWORD* imageData = (DWORD*)lockedRect.pBits; for(int i = 0; i < textureDesc.Height; i++) { for(int j = 0; j < textureDesc.Width; j++) { int index = i * lockedRect.Pitch / 4 + j;

// Получаем текущий цвет ячейки D3DXCOLOR c(imageData[index]);

// Затеняем текущую ячейку c *= computeShade(i, j, lightDirection);;

// Сохраняем затененный цвет imageData[index] = (D3DCOLOR)c; } }